Сложные проценты (или «проценты на проценты») – это метод расчета дохода кредитора, при котором процентный платеж в каждом расчетном периоде добавляется к капиталу предыдущего периода, а в следующем периоде проценты начисляются уже на наращенный капитал.
В этом случае происходит капитализация процентов, т. е. присоединение начисленных процентов к их базе и, следовательно, база, с которой начисляются проценты, все время возрастает.
Если процентный платеж начисляется и добавляется к капиталу один раз в год, то считается, что капитализация является годовой.
Если процентный платеж начисляется и добавляется к капиталу каждые 6 месяцев, то это называется полугодовой капитализацией.
Начисление сложных процентов и их капитализация может производится поквартально, каждый месяц и т.д.
Существуют два способа начисления сложных процентов: антисипативное (предварительное) и декурсивное (последующее).
Антисипативное начисление сложных процентов – это начисление процентов в начале каждого расчетного периода. Этот способ используется в период высокой инфляции.
Декурсивное начисление сложных процентов – это начисление процентов в конце каждого расчетного периода. Это наиболее распространенный способ начисления сложных процентов.
При декурсивном способе расчета конечная стоимость капитала может быть рассчитана по следующей формуле:
Fn = P * (1 + r) n
где Fn - конечная стоимость капитала
P - первоначальная стоимость капитала
r – процентная ставка, выраженная в десятичных дробях
n – число периодов начисления
Величина (1 + r) называется декурсивным коэффициентом, а n–я степень этого коэффициента – коэффициентом наращивания.
Совокупный процентный платеж при декурсивном начислении можно рассчитать по следующей формуле:
I = P * [ (1 + r) n – 1]
Из выше перечисленных формул можно найти процентную ставку и период:
r = 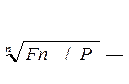 1
1
n =(log Fn – log P) / log (1 + r)
При антисипативном начислении сложных процентов конечную сумму капитала можно рассчитать по следующей формуле:
Fn = P * [ 1 / (1 – r)] n
Отсюда при необходимости можно найти I, r, n
I = F – P = P*[ 1 / (1 – r)] n - P = P * ([1 / (1 – r)] n – 1)
 2014-02-24
2014-02-24 3832
3832
