При использовании сложных процентов база для начисления процентов увеличивается от периода к периоду, т.е. процесс наращения капитала происходит с ускорением. Механизм возрастания капитала по сложным процентам называют капитализацией. Различают годовую капитализацию, полугодовую, квартальную, месячную и ежедневную.
Наращенная сумма сложных декурсивных процентов определяется по формуле:
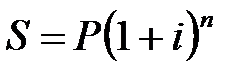 , (2.1)
, (2.1)
где P – первоначальная величина капитала (кредита, депозита, ссуды и т.д.),
S – наращенная сумма капитала на конец срока финансовой операции,
n – срок финансовой операции, лет,
i – годовая ставка процентов, выраженная десятичной дробью.
Сумма начисленных процентов I составляет:
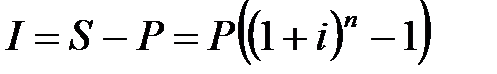 . (2.2)
. (2.2)
Если используются переменные значения процентной ставки во времени, то наращенная сумма определяется по формуле:
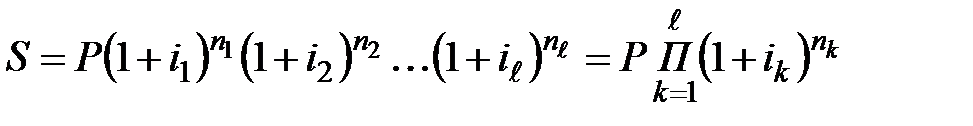 , (2.3)
, (2.3)
где 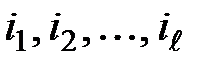 – последовательные значения переменной процентной ставки,
– последовательные значения переменной процентной ставки,
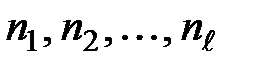 – продолжительность периодов (лет), к которым приурочены соответствующие значения процентной ставки,
– продолжительность периодов (лет), к которым приурочены соответствующие значения процентной ставки,
ℓ – число значений процентной ставки.
Часто срок финансовой операции является не целым, а дробным числом. Для определения наращенной суммы капитала в этом случае используют два метода:
а) общий 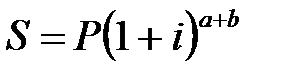 , (2.4)
, (2.4)
б) смешанный 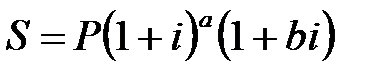 , (2.5)
, (2.5)
где 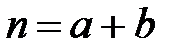 – срок финансовой операции, лет;
– срок финансовой операции, лет; 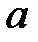 – целое число лет,
– целое число лет, 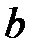 – дробная часть года.
– дробная часть года.
Аналогичный метод применяется и в случаях, когда периодом начисления является полугодие, квартал или месяц, а также при использовании учетной ставки d.
Множитель наращения по смешанному методу оказывается несколько больше, чем по общему.
Проценты капитализируются не только один, а несколько раз в году – по полугодиям, кварталам, месяцам (даже ежедневно). В контрактах при этом указывается не ставка за период начисления (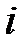 ), а годовая ставка (
), а годовая ставка ( ), одновременно указывается период начисления процентов. Годовая процентная ставка j называется номинальной.
), одновременно указывается период начисления процентов. Годовая процентная ставка j называется номинальной.
Формула наращения процентов при этом имеет вид:
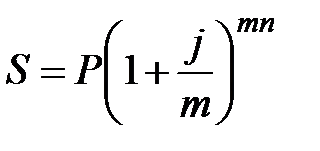 , (2.6)
, (2.6)
где 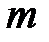 – число начисления процентов в году (ежегодное начисление m = 1; по полугодиям, m = 2; ежеквартальное, m = 4; ежемесячное, m = 12; ежедневное, m= 365).
– число начисления процентов в году (ежегодное начисление m = 1; по полугодиям, m = 2; ежеквартальное, m = 4; ежемесячное, m = 12; ежедневное, m= 365).
Наращение по сложной учетной ставке осуществляется по формулам:
а) при ежегодном начислении процентов (m =1)
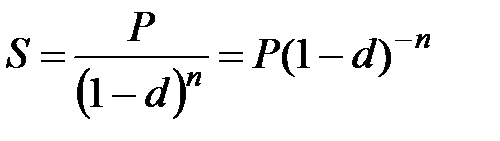 ; (2.7)
; (2.7)
б) при m -разовом начислении процентов (m >1)
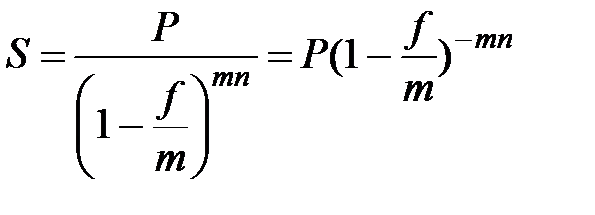 . (2.8)
. (2.8)
Если используются переменные значения учетной ставки, то наращенная сумма определяется по формуле:
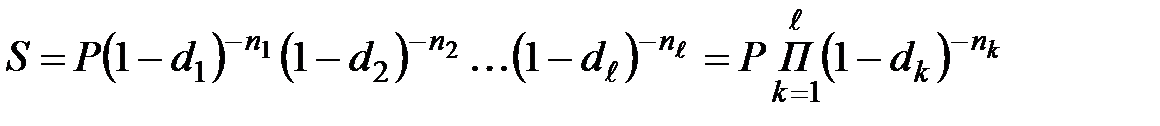 . (2.9)
. (2.9)
Дисконтирование по сложной ставке процента может быть математическим и банковским.
Математическое дисконтирование заключается в определении современной величины капитала P по значению наращенной суммы S с использованием сложной ставки декурсивных процентов. Современная стоимость капитала составит:
а) при ежегодном начислении процентов
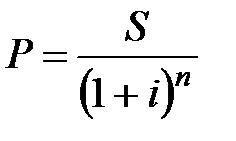 ; (2.10)
; (2.10)
б) при m -разовом начислении процентов в году
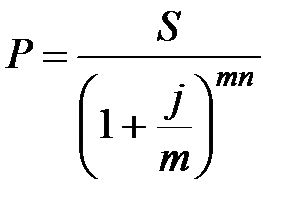 . (2.11)
. (2.11)
Банковское дисконтирование по сложной учетной ставке может быть использовано при учете среднесрочных и долгосрочных долговых обязательств. Дисконтированная величина долгового обязательства составит:
а) при ежегодном начислении процентов
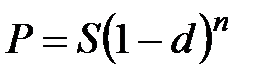 ; (2.12)
; (2.12)
б) при m -разовом начислении процентов
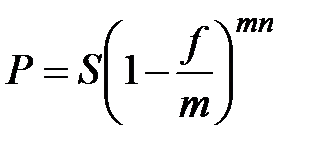 . (2.13)
. (2.13)
Таблица 2.1 - Определение срока финансовой операции и ставки процента
| Декурсивные проценты | Антисипативные проценты | ||
| m =1 | m >1 | m =1 | m >1 |
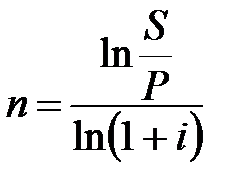 (2.14) (2.14) | 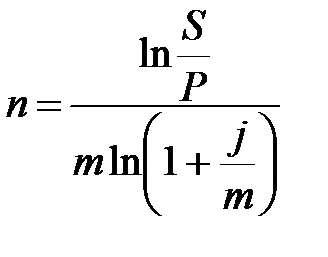 (2.16) (2.16) | 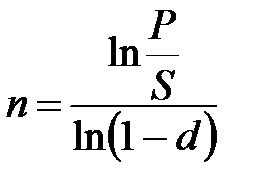 (2.18) (2.18) | 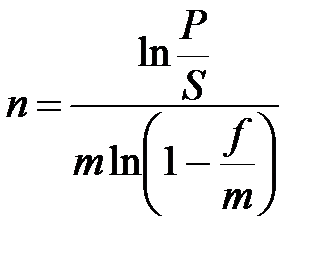 (2.20) (2.20) |
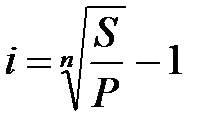 (2.15) (2.15) | 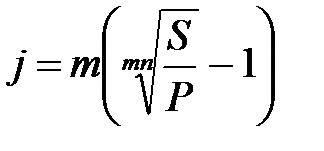 (2.17) (2.17) | 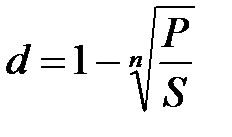 (2.19) (2.19) | 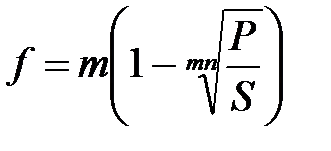 (2.21) (2.21) |
При непрерывном наращении процентов применяют силу роста, которая характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.
Постоянная сила роста (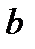 ) представляет собой номинальную ставку сложных процентов при
) представляет собой номинальную ставку сложных процентов при 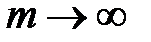 . Наращенная сумма капитала составит
. Наращенная сумма капитала составит
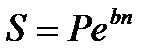 , (2.22)
, (2.22)
а современная стоимость 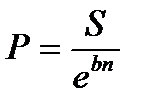 . (2.23)
. (2.23)
Переменная сила роста (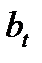 ) изменяется во времени, следуя закону, представленному в виде непрерывной функции времени
) изменяется во времени, следуя закону, представленному в виде непрерывной функции времени 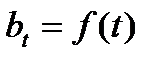 .
.
Линейная функция:
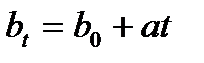 , (2.24)
, (2.24)
где 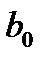 – начальное значение силы роста, а – прирост силы роста в единицу времени.
– начальное значение силы роста, а – прирост силы роста в единицу времени.
Наращенная сумма капитала составит:
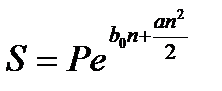 , (2.25)
, (2.25)
а современная стоимость:
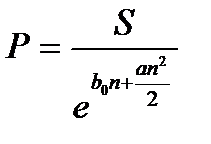 . (2.26)
. (2.26)
Экспоненциальная функция:
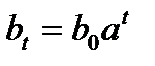 , (2.27)
, (2.27)
где 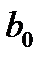 – начальное значение силы роста, а – постоянный коэффициент роста.
– начальное значение силы роста, а – постоянный коэффициент роста.
Наращенная сумма капитала составит:
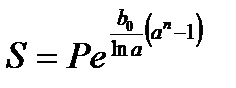 , (2.28)
, (2.28)
а современная стоимость:
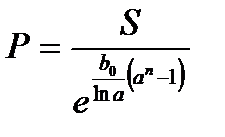 . (2.29)
. (2.29)
Таблица 2.2 - Определение срока финансовой операции и силы роста
| Постоянная сила роста | Переменная сила роста (экспоненциальная) |
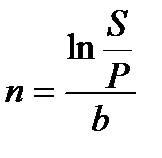 (2.30) (2.30) | 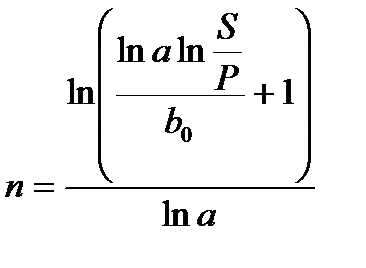 (2.32) (2.32) |
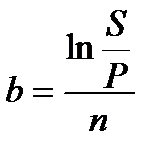 (2.31) (2.31) | 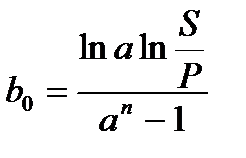 (2.33) (2.33) |
Налогообложение процентного дохода уменьшает реальную наращенную сумму и доходность депозитной операции. Если начисляются простые проценты, то сумма налога на проценты L за весь срок финансовой операции составит:
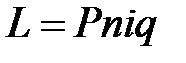 , (2.34)
, (2.34)
где q – ставка налога на проценты.
Наращенная сумма с учетом выплаты налога:
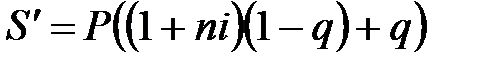 . (2.35)
. (2.35)
При долгосрочных операциях и начислении сложных процентов сумма налога на проценты определяется по формуле:
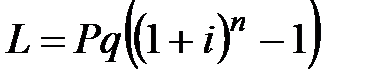 . (2.36)
. (2.36)
Наращенная сумма с учетом выплаты налога:
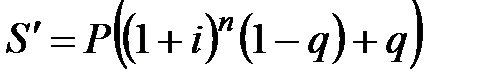 . (2.37)
. (2.37)
Сумма налога на проценты 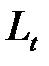 за каждый год отдельно составляет:
за каждый год отдельно составляет:
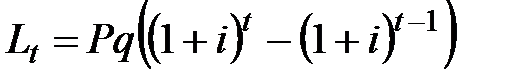 , (2.38)
, (2.38)
где t – порядковый номер года.
Наращенная сумма с учетом влияния инфляции (C) по схеме простых процентов определяется по формулам:
а) декурсивные проценты
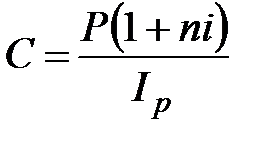 ; (2.39)
; (2.39)
б) антисипативные проценты
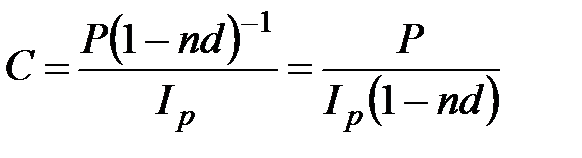 , (2.40)
, (2.40)
где 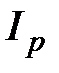 – индекс цен за соответствующий период n (эту величину также называют индексом инфляции за период n).
– индекс цен за соответствующий период n (эту величину также называют индексом инфляции за период n).
Соответственно, темп прироста инфляции hn за период времени n лет составит: 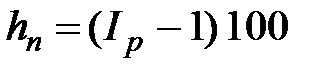 . (2.41)
. (2.41)
Индекс инфляции 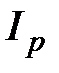 за весь период в n лет при известных темпах прироста инфляции за составляющие его подпериоды:
за весь период в n лет при известных темпах прироста инфляции за составляющие его подпериоды:
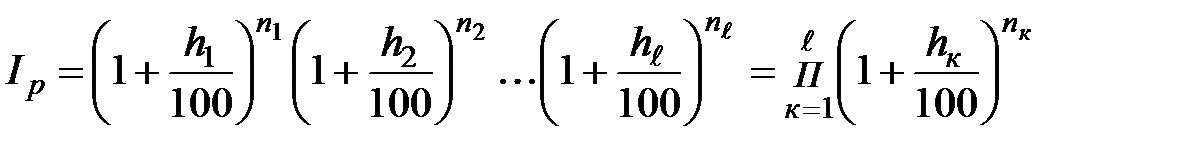 , (2.42)
, (2.42)
где  – темпы прироста инфляции за соответствующие подпериоды, %;
– темпы прироста инфляции за соответствующие подпериоды, %;
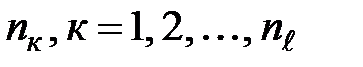 – период действия соответствующего темпа прироста
– период действия соответствующего темпа прироста
инфляции, 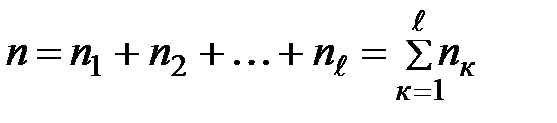 .
.
Наращенная сумма с учетом влияния инфляции по схеме сложных процентов определяется по формулам:
а) декурсивные проценты
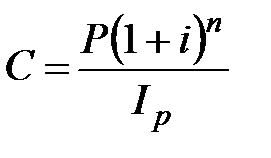 , при m =1;
, при m =1; 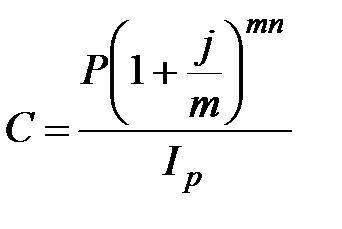 , при m >1; (2.43)
, при m >1; (2.43)
б) антисипативные проценты
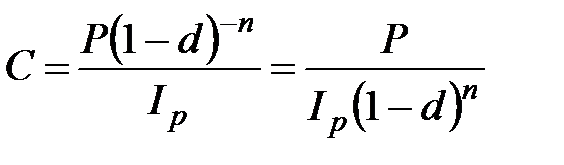 , при m =1; (2.44)
, при m =1; (2.44)
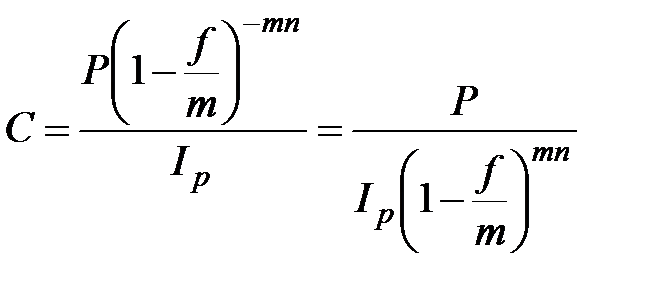 , при m >1; (2.45)
, при m >1; (2.45)
в) непрерывные проценты
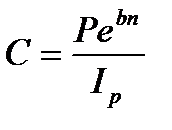 . (2.46)
. (2.46)
Реальная доходность финансовой операции с учетом инфляции измеряется с помощью соответствующих ставок процента:
а) по схеме простых процентов
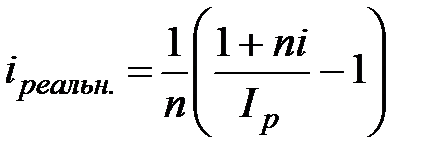 ;
; 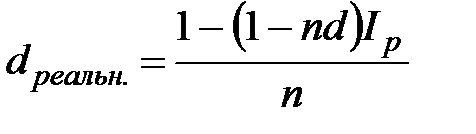 ; (2.47)
; (2.47)
б) по схеме сложных процентов
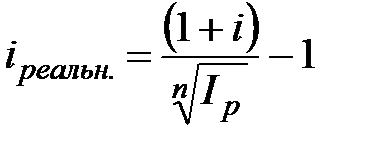 ,
, 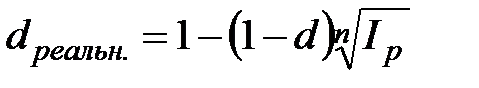 , при m =1; (2.48)
, при m =1; (2.48)
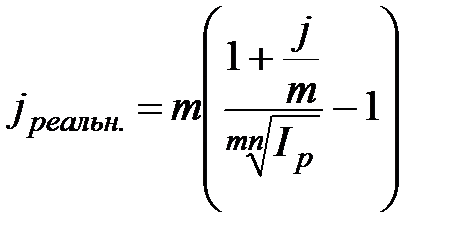 ,
, 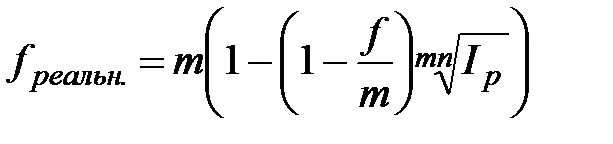 , при m >1; (2.49)
, при m >1; (2.49)
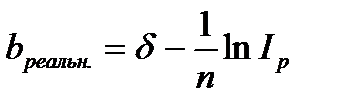 ,
, 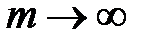 . (2.50)
. (2.50)
Минимальная ставка процента, нейтрализующая действие инфляции, определяется из равенства индекса инфляции и соответствующего множителя наращения. Если начисляются сложные декурсивные проценты по ставке i за n лет, а индекс инфляции за этот же период составил 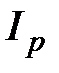 , то:
, то:
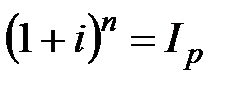 , откуда
, откуда 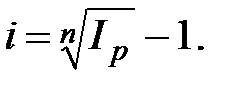 (2.51)
(2.51)
Для обеспечения реального наращения капитала в условиях инфляции должно выполняться неравенство 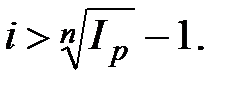
В целях компенсации потерь от снижения покупательной способности денег ставку процента корректируют с учетом темпа инфляции. Величина корректирующей брутто-ставки r, которая обеспечивает реальную доходность финансовой операции по заданной ставке процента, определяется по формулам:
а) по схеме простых процентов
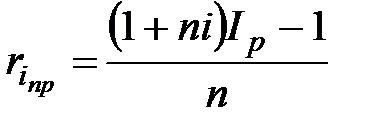 ;
; 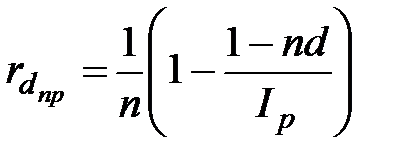 ; (2.52)
; (2.52)
б) по схеме сложных процентов
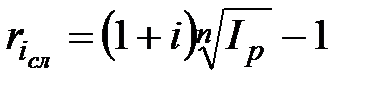 ,
, 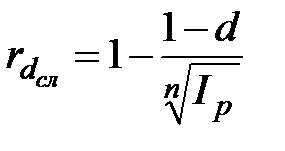 , при m =1; (2.53)
, при m =1; (2.53)
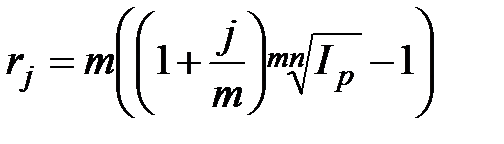 ,
, 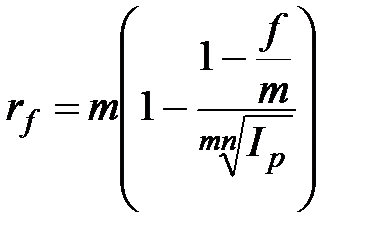 , при m >1; (2.54)
, при m >1; (2.54)
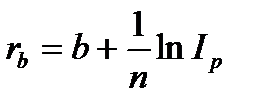 ,
, 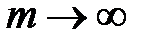 . (2.55)
. (2.55)
Пример 2.1 Сумма 200 тыс. руб. инвестируется под процентную ставку 15 % годовых: 1) на 3 месяца; 2) на 6 месяцев; 3) на 1 год; 4) на 6 лет; 5) на 9 лет. Найти наращенные суммы по схеме простых и сложных процентов.
Решение.
1. По условию задачи n1 =0,25 года, n2 =0,5 года, n3 =1 год, n4 =6 лет, n5 =9 лет, P =200000 руб., i =0,15. При наращении простых процентов по формуле (1.2) получим:
1.1. 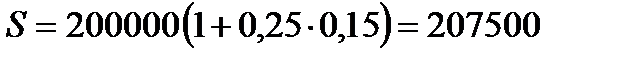 руб.
руб.
1.2. 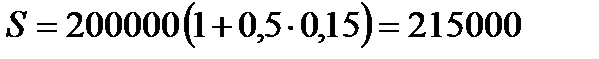 руб.
руб.
1.3. 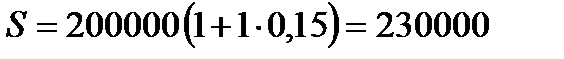 руб.
руб.
1.4. 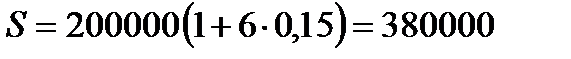 руб.
руб.
1.5. 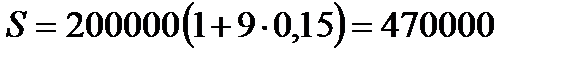 руб.
руб.
2. При наращении сложных процентов по формуле (2.1) получим:
2.1. 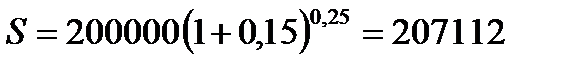 руб.
руб.
2.2. 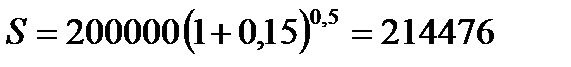 руб.
руб.
2.3. 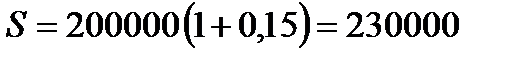 руб.
руб.
2.4. 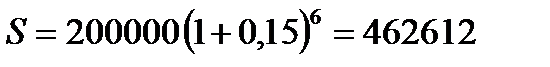 руб.
руб.
2.5. 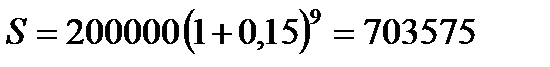 руб.
руб.
Для владельца капитала более выгодной является схема простых декурсивных процентов, если срок финансовой операции менее одного года; схема сложных декурсивных процентов – если срок превышает один год. При однократном начислении процентов и продолжительности периода один год обе схемы дают равные результаты.
Пример 2.2 В банке получена ссуда в размере 400 тыс. руб. на 8 лет на следующих условиях: для первых трех лет процентная ставка равна 10% годовых, на следующий год устанавливается маржа в размере 1%, а на последующие годы маржа равна 1,5%. Найдите сумму, которая должна быть возвращена банку по окончании срока ссуды при ежегодных начислениях сложных процентов.
Решение. Поскольку имеем дело с переменной процентной ставкой, то P =400000 руб., n1 =3, n2 =1, n3 =4, i1 =0,10, i2 =0,11, i3 =0,115. Используя формулу 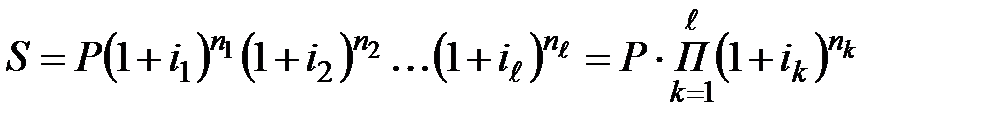 , получим:
, получим:
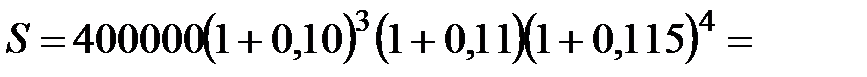 913398,92 руб.
913398,92 руб.
Пример 2.3 Предприниматель получил в банке ссуду в размере 50 тыс. руб. на 39 месяцев под процентную ставку 17% годовых на условиях начисления процентов: а) ежегодного; б) полугодичного. Какую сумму предприниматель должен будет вернуть банку по истечении срока при использовании схемы: сложных процентов, смешанной?
 2015-01-07
2015-01-07 3656
3656
