Полный дифференциал 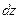 функции называют также дифференциалом первого порядка.
функции называют также дифференциалом первого порядка.
Пусть функция 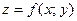 имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле
имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле 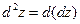 . Найдем его:
. Найдем его:
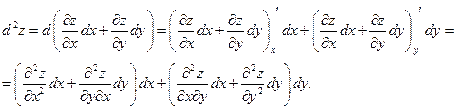
Отсюда:
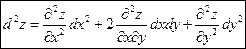 .
.
Символически это записывается так:
 .
.
Аналогично можно получить формулу для дифференциала третьего порядка:
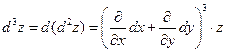 ,
,
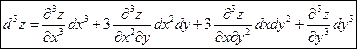 .
.
Дифференциал любого порядка 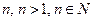 определяется равенством
определяется равенством
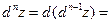
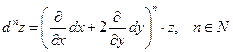 .
.
Методом математической индукции можно доказать, что формула для его вычисления в случае функции двух переменных и равенства их соответствующих смешанных производных аналогична формуле бинома Ньютона.
Для функции трех переменных дифференциал второго порядка записывается аналогично формуле 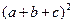 .
.
 2014-02-24
2014-02-24 1419
1419








