Понятия локального и глобального экстремумов функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.
Пусть функция 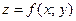 определена в некоторой области
определена в некоторой области 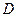 , точка
, точка 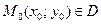 .
.
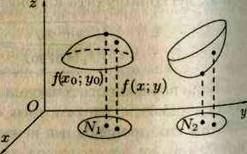
Определение 1. Точка 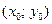 называется точкой максимума функции
называется точкой максимума функции 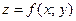 , если существует такая
, если существует такая 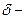 окрестность точки
окрестность точки 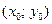 , что для каждой точки
, что для каждой точки 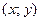 , отличной от
, отличной от 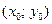 , из этой окрестности выполняется неравенство
, из этой окрестности выполняется неравенство 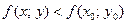 .
.
|
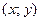 , отличных от
, отличных от 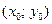 , из
, из 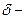 окрестности точки
окрестности точки 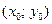 выполняется неравенство:
выполняется неравенство: 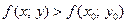 .
.
Определение 3. Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции.
Отметим, что в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке 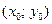 сравнивается с ее значениями в точках, достаточно близких к
сравнивается с ее значениями в точках, достаточно близких к 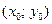 . В области
. В области 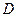 функция может иметь несколько экстремумов или не иметь ни одного.
функция может иметь несколько экстремумов или не иметь ни одного.
Рассмотрим условия существования экстремума функции.
Теорема 1 (необходимые условия экстремума). Если в точке 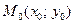 дифференцируемая функция
дифференцируемая функция 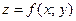 имеет экстремум, то ее частные производные в этой точке равны нулю:
имеет экстремум, то ее частные производные в этой точке равны нулю:
 .
.
Геометрически равенства 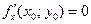 и
и 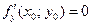 означают, что в точке экстремума функции
означают, что в точке экстремума функции 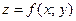 касательная плоскость к поверхности, изображающей функцию
касательная плоскость к поверхности, изображающей функцию 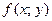 , параллельна плоскости
, параллельна плоскости 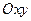 , т.к. уравнение касательной плоскости есть
, т.к. уравнение касательной плоскости есть 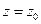 .
.
Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция 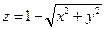 имеет максимум в точке
имеет максимум в точке 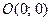 , но не имеет в этой точке частных производных.
, но не имеет в этой точке частных производных.
Определение 1. Точка, в которой частные производные первого порядка функции 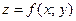 равны нулю, т.е.
равны нулю, т.е. 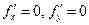 , называется стационарной точкой функции
, называется стационарной точкой функции 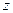 .
.
Определение 2. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическим точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию 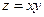 . Для нее точка
. Для нее точка 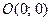 является критической (в ней
является критической (в ней 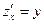 и
и 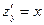 обращаются в ноль). Однако экстремума в ней функция
обращаются в ноль). Однако экстремума в ней функция 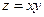 не имеет, т.к. в достаточно малой окрестности точки
не имеет, т.к. в достаточно малой окрестности точки 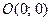 найдутся точки для которых
найдутся точки для которых 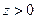 (точки I и III четвертей) и
(точки I и III четвертей) и 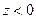 (точки II и IV четвертей).
(точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 2 (достаточное условие экстремума). Пусть в стационарной точке 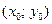 и некоторой ее окрестности функция
и некоторой ее окрестности функция 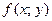 имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке
имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 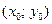 значения
значения 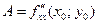 ,
, 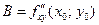 ,
, 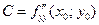 . Обозначим
. Обозначим
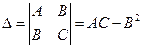 .
.
Тогда:
1) если 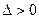 , то функция
, то функция 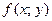 в точке
в точке 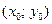 имеет экстремум: максимум, если
имеет экстремум: максимум, если 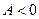 ; минимум, если
; минимум, если 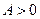 ;
;
2) если 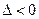 , то функция
, то функция 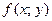 в точке
в точке 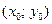 экстремума не имеет;
экстремума не имеет;
3) в случае 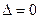 экстремум в точке
экстремум в точке 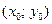 может быть, может не быть. Необходимы дополнительные исследования.
может быть, может не быть. Необходимы дополнительные исследования.
 2014-02-24
2014-02-24 1280
1280

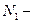 точка максимума, а
точка максимума, а 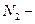 точка минимума функции
точка минимума функции