Функция 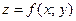 называется неявной, если она задается уравнением
называется неявной, если она задается уравнением
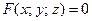 (1)
(1)
неразрешенным относительно 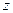 . Найдем частные производные
. Найдем частные производные 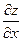 и
и 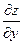 неявной функции
неявной функции 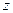 , заданной уравнением (1). Для этого, подставив в уравнение вместо
, заданной уравнением (1). Для этого, подставив в уравнение вместо 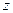 функцию
функцию 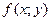 , получим тождество
, получим тождество
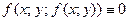 .
.
Частные производные по 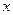 и по
и по 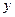 функции, тождественно равной нулю, также равны нулю:
функции, тождественно равной нулю, также равны нулю:
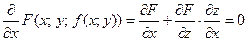 (
(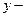 считаем постоянным),
считаем постоянным),
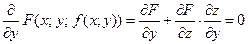 (
(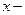 считаем постоянным),
считаем постоянным),
откуда
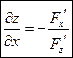 и
и 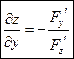 ,
, 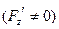 . (2)
. (2)
Замечания.
1. Уравнение вида (1) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение 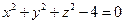 определяет функции
определяет функции 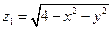 и
и 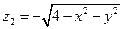 , определенные в круге
, определенные в круге 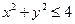 ,
, 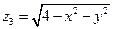 , определенную в полукруге
, определенную в полукруге 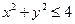 при
при 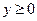 и т.д., а уравнение
и т.д., а уравнение 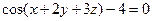 не определяет никакой функции.
не определяет никакой функции.
Теорема существования неявной функции двух переменных: если функция 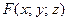 и ее производные
и ее производные 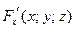 ,
, 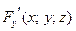 ,
, 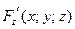 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 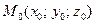 , причем
, причем 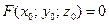 , а
, а 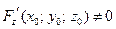 , то существует окрестность точки
, то существует окрестность точки 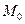 , в которой уравнение (1) определяет единственную функцию
, в которой уравнение (1) определяет единственную функцию 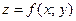 , непрерывную и дифференцируемую в окрестности точки
, непрерывную и дифференцируемую в окрестности точки 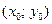 и такую, что
и такую, что 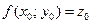 .
.
2. Неявная функция 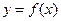 одной переменной задается уравнением
одной переменной задается уравнением 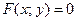 . Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
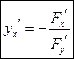 (
(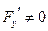 ).
).
 2014-02-24
2014-02-24 1150
1150
