Пусть 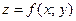 – функция двух переменных
– функция двух переменных 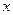 и
и 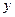 , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной 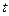 :
: 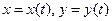 . В этом случае функция
. В этом случае функция 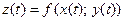 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной 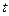 ; переменные
; переменные 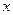 и
и 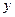 – промежуточные переменные.
– промежуточные переменные.
Теорема. Если 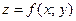 – дифференцируемая в точке
– дифференцируемая в точке 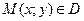 функция и
функция и 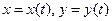 – дифференцируемые функции независимой переменной
– дифференцируемые функции независимой переменной 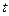 , то производная сложной функции
, то производная сложной функции 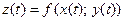 вычисляется по формуле
вычисляется по формуле
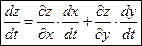 . (1)
. (1)
Частный случай: 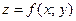 , где
, где  , т.е.
, т.е. 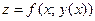 – сложная функция одной независимой переменной
– сложная функция одной независимой переменной 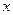 . Этот случай сводится к предыдущему, причем роль переменной
. Этот случай сводится к предыдущему, причем роль переменной 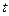 играет
играет 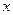 . Согласно формуле (1) имеем:
. Согласно формуле (1) имеем:
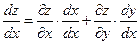
или
 . (2)
. (2)
Формула (2) носит название формулы полной производной.
Общий случай: 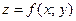 , где
, где 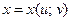 ,
, 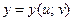 . Тогда
. Тогда  – сложная функция независимых переменных
– сложная функция независимых переменных 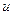 и
и 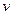 . Ее частные производные
. Ее частные производные  и
и  можно найти, используя формулу (1) следующим образом. Зафиксировав
можно найти, используя формулу (1) следующим образом. Зафиксировав 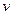 , заменяем в ней
, заменяем в ней 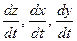 соответствующими частными производными
соответствующими частными производными 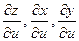 :
:
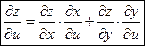 (3)
(3)
Аналогично получаем:
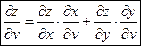 .
.
Таким образом, производная сложной функции (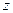 ) по каждой независимой переменной (
) по каждой независимой переменной (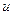 и
и 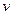 ) равна сумме произведений частных производных этой функции (
) равна сумме произведений частных производных этой функции (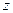 ) по ее промежуточным переменным (
) по ее промежуточным переменным (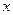 и
и 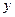 ) на их производные по соответствующей независимой переменной (
) на их производные по соответствующей независимой переменной (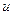 и
и 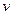 ).
).
|
|
|
 2014-02-24
2014-02-24 4979
4979
