2014-02-24
992
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция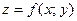 
дифференцируема в точке 
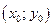некоторой области 
.
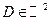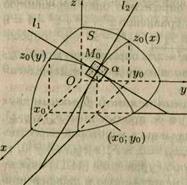
Проводя аналогичные рассуждения для сечения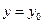 
, построим касательную 
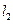к кривой
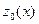в точке 
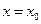. Прямые 
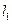и 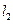определяют плоскость 
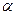, которая называется касательной плоскостью к поверхности S в точке 
.
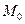Составим ее уравнение. Так как плоскость 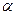проходит через точку 
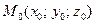, то ее уравнение может быть записано в виде
,
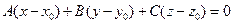которое можно переписать так:
.
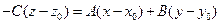Разделив уравнение на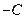 
и обозначив 
, 
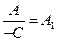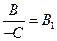получим
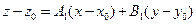. (1)
Найдем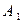 
и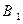 
.
Уравнения касательных 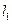и 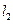имеют вид
;
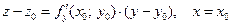соответственно.
Касательная 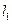лежит в плоскости 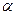, следовательно, координаты всех точек 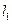удовлетворяют уравнению (1). Этот факт можно записать в виде системы
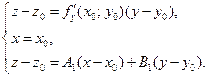
Разрешая эту систему относительно 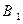, получим, что 
.
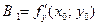Проводя аналогичные рассуждения для касательной 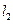, легко установить, что 
.
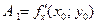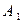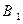Подставив значения и в уравнение (1), получаем искомое уравнение касательной плоскости:
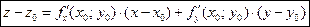. (2)
Определение. Прямая, проходящая через точку 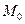и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
Используя условие перпендикулярности прямой и плоскости, легко получить канонические уравнения нормали:
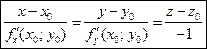. (3)
Если поверхность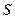 
задана уравнением 
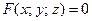, то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
, 
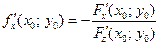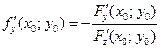
примут соответственно вид
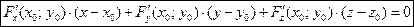
и
.
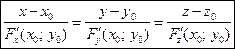Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т.е. не особых, точек поверхности. Точка 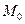поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
