Пусть функция 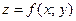 определена и непрерывна в ограниченной замкнутой области
определена и непрерывна в ограниченной замкнутой области 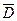 . Тогда она достигает в некоторых точках
. Тогда она достигает в некоторых точках 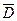 своего наибольшего
своего наибольшего 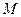 и наименьшего
и наименьшего 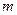 значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области
значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области 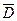 , или в точках, лежащих на границе области.
, или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области 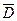 функции
функции 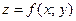 состоит в следующем:
состоит в следующем:
1. Найти все критические точки функции, принадлежащие 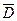 , и вычислить значения функции в них;
, и вычислить значения функции в них;
2. Найти наибольшее и наименьшее значения функции 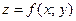 на границах области;
на границах области;
3. Сравнить все найденные значения функции и выбрать из них наибольшее 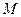 и наименьшее
и наименьшее 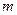 .
.
 2014-02-24
2014-02-24 569
569








