Рассмотрим случай приобретения двух видов благ A и B в условиях ограниченного бюджета. Пусть потребитель обладает денежными ресурсами в объеме R и намерен израсходовать их на приобретение благ видов A и B предлагаемых на рынке по ценам 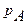 и
и 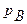 . При этом процесс приобретения благ разбит на n шагов, на каждом из которых покупатель расходует одинаковую порцию денежных ресурсов
. При этом процесс приобретения благ разбит на n шагов, на каждом из которых покупатель расходует одинаковую порцию денежных ресурсов 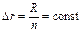 . На каждом шаге необходимо принять решение о приобретении очередной порции блага либо вида A либо B.
. На каждом шаге необходимо принять решение о приобретении очередной порции блага либо вида A либо B.
Возникает вопрос: каким образом следует распределить имеющие ресурсы в объеме R, чтобы получить максимальную совокупную полезность 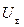 от приобретения благ.
от приобретения благ.
Пусть 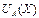 – функция совокупной полезности при приобретении блага A в количестве Х,
– функция совокупной полезности при приобретении блага A в количестве Х, 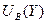 – блага B в количестве Y. Тогда ограничение по денежным ресурсам примет вид:
– блага B в количестве Y. Тогда ограничение по денежным ресурсам примет вид: 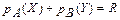 .
.
Будем считать, что блага А и В не являются взаимозаменяемыми или взаимодополняемыми, то есть функция 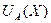 не зависит от Y, а функцию
не зависит от Y, а функцию 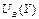 не зависит от Х. Если на конкретном шаге покупатель принял решение приобрести благо А в количестве
не зависит от Х. Если на конкретном шаге покупатель принял решение приобрести благо А в количестве 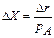 , то прирост полезности составит
, то прирост полезности составит 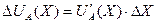 .
.
Если принято решение приобрести благо вида B в количестве 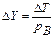 , то прирост полезности составит
, то прирост полезности составит 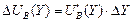 .
.
Очевидно, при этом предпочтение надо отдать такому виду блага, который обеспечит больший прирост полезности 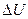 . Например, условием приобретения блага A на очередном шаге является условие:
. Например, условием приобретения блага A на очередном шаге является условие:
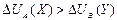 (3) или
(3) или 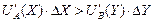
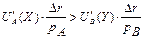 или
или 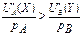 (4)
(4)
Отношение 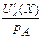 называют предельной полезностью блага вида A в расчете на единицу затрат ресурса (предельная полезность блага A на одну затраченную для этого денежную единицу).
называют предельной полезностью блага вида A в расчете на единицу затрат ресурса (предельная полезность блага A на одну затраченную для этого денежную единицу).
Т.о., неравенство (4) дает критерий выбора потребителем вида A или B потребляемого блага, согласно которому на каждом шаге использования денежного ресурса в объеме 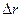 предпочтение нужно отдать приобретению такого вида блага, предельная полезность которого в расчете на единицу затрат ресурса больше.
предпочтение нужно отдать приобретению такого вида блага, предельная полезность которого в расчете на единицу затрат ресурса больше.
Пока выполняется условие (3) потребитель будет увеличивать объем Х потребления блага A, снижая при этом предельную полезность 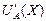 этого блага до тех пор, пока на некотором шаге не возникнет ситуация
этого блага до тех пор, пока на некотором шаге не возникнет ситуация 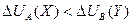 , и тогда потребитель начнет приобретать другое благо – благо вида B.
, и тогда потребитель начнет приобретать другое благо – благо вида B.
Т.о. многократно используя критерий (3,4), потребитель стремится уравнять 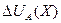 и
и 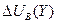 , т.е. достичь условия потребительского равновесия:
, т.е. достичь условия потребительского равновесия: 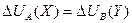 (5) или
(5) или 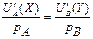 (6).
(6).
Известно что, если на последнем шаге расходования денежного ресурса R потребителю удалось достичь условия равновесия (5-6), то он обеспечивает себе оптимальный вариант 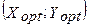 приобретения благ видов A и B, и получить максимум совокупной полезности max
приобретения благ видов A и B, и получить максимум совокупной полезности max 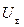 при заданном бюджетном ограничении R.
при заданном бюджетном ограничении R.
Величины 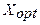 и
и 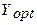 являются корнями системы уравнений
являются корнями системы уравнений 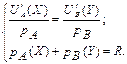
 2014-02-09
2014-02-09 441
441








