Задача 1. Дана функция полезности U (X) блага Х. Определить:
1) максимальное количество блага х 0, которое выгодно приобрести потребителю при рыночной цене р 0 этого блага;
2) максимальную величину «дополнительной выгоды потребителя» 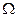 от приобретения данного блага;
от приобретения данного блага;
3) выгодно ли потребителю приобретать очередную порцию блага по цене р 1, если он уже обладает этим благом в количестве х 1единиц;
4) рыночную цену р 2 блага, чтобы потребитель приобрел не более х 2единиц этого блага.
Случай 1 Рассмотрим степенную модель функции совокупной полезности: 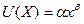 (
(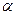 >0, 0<
>0, 0<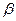 <1).
<1).
Пусть 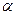 = 5,
= 5, 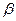 = 0,15; р 0=0,5, х 1=1,3; р 1=1,4, х 2=1,5. Тогда имеем
= 0,15; р 0=0,5, х 1=1,3; р 1=1,4, х 2=1,5. Тогда имеем 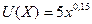 .
.
1. Найдем максимальное количество блага х 0 из условия 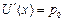 . Имеем:
. Имеем: 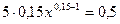 Þ х =1,6112.
Þ х =1,6112.
2. Величину предельной выгоды 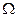 найдем по формуле
найдем по формуле 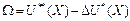 , где
, где 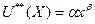 - совокупная полезность данного запаса блага,
- совокупная полезность данного запаса блага, 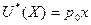 - затраты на приобретение этого запаса благ. Тогда
- затраты на приобретение этого запаса благ. Тогда
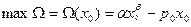 ;
; 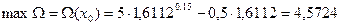 .
.
3. Потребителю выгодно приобрести дополнительную порцию блага по цене р 1=1,4, когда он уже обладает этим благом в количестве х 1=1,3 единиц, если выполняется условие: 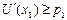 , т.е.
, т.е. 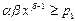 Þ
Þ 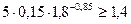 Þ 0,6
Þ 0,6 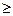 1,4 - ложь. Условие
1,4 - ложь. Условие 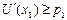 не выполняется, следовательно потребителю не выгодно приобрести дополнительную порцию блага по цене 1,4, если он уже обладает этим благом в количестве 1,3 единиц.
не выполняется, следовательно потребителю не выгодно приобрести дополнительную порцию блага по цене 1,4, если он уже обладает этим благом в количестве 1,3 единиц.
4. Потребитель приобретет не более х 2=1,5 единиц блага, если значение рыночной цены р 2 блага удовлетворяют условию 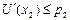 . В рассматриваемом случае
. В рассматриваемом случае 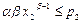 , т.е.
, т.е. 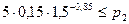 Þ
Þ 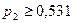 . Т.о. при рыночной цене р 2
. Т.о. при рыночной цене р 2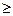 0,531 потребителю выгодно приобрести не более 1,5 единиц данного блага.
0,531 потребителю выгодно приобрести не более 1,5 единиц данного блага.
Задача 2. Найти оптимальную структуру потребления благ видов A и B, реализуемых на рынке по ценам 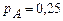 и
и 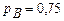 , если функции совокупных полезностей этих благ имеют вид
, если функции совокупных полезностей этих благ имеют вид 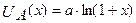 и
и 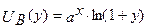 соответственно, а выделенный на приобретение этих благ ресурс равен R =2,5 (х –количество потребляемого блага A, y – количество потребляемого блага В). a = 2,
соответственно, а выделенный на приобретение этих благ ресурс равен R =2,5 (х –количество потребляемого блага A, y – количество потребляемого блага В). a = 2, 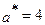 .
.
По условию задачи 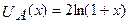 ;
; 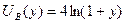 . Тогда
. Тогда 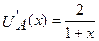 ,
, 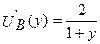 .
.
Бюджетные ограничения описываются уравнением: 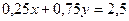 или
или 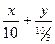 =1.
=1.
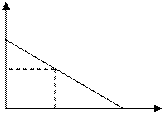 Оптимальную структуру потребления
Оптимальную структуру потребления 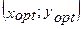 благ А и В найдем из системы
благ А и В найдем из системы
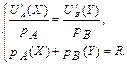 Имеем Имеем 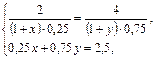 откуда откуда 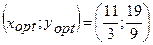 . Т.о., оптимальный объем потребления блага А составляет . Т.о., оптимальный объем потребления блага А составляет 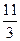 ед., а блага В - ед., а блага В - 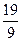 ед. ед. |  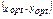 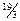 Бюджетная линия Бюджетная линия 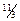 10 10 |
 2014-02-09
2014-02-09 1419
1419








