Рассмотрим наиболее распространенные экономические модели закона убывающей предельной полезности, когда функция совокупной полезности U (X) возрастает с убывающей скоростью, а предельная полезность 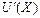 – убывает с убывающей скоростью.
– убывает с убывающей скоростью.
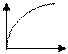 Модель 1.Совокупная полезность U (X) неограниченно растет с увеличением количества блага Х (деньги, земельные участки, предметы роскоши, жилье и т.д.). При этом U (0)=0, U ( Модель 1.Совокупная полезность U (X) неограниченно растет с увеличением количества блага Х (деньги, земельные участки, предметы роскоши, жилье и т.д.). При этом U (0)=0, U (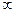 ) = ) = 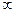 . Этим условиям удовлетворяют:
а) степенная модель: . Этим условиям удовлетворяют:
а) степенная модель: 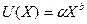 ( (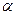 >0, 0< >0, 0<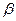 <1); (1)
б) логарифмическая модель: <1); (1)
б) логарифмическая модель: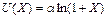 ( (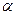 >0). (2) >0). (2)
| Модель 2.Совокупная полезность U (X) стремится к некоторому пределу А при Х 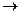 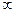 , U (0) = 0. Этим условиям удовлетворяют:
1) экспоненциальная модель , U (0) = 0. Этим условиям удовлетворяют:
1) экспоненциальная модель 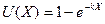 (k >0) (3)
2) дробно-рациональная модель (k >0) (3)
2) дробно-рациональная модель 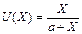 (a >0) (4) (a >0) (4)
 Подобные модели применяют при рассмотрении таких благ, как пища, одежда, обувь и т.п. Подобные модели применяют при рассмотрении таких благ, как пища, одежда, обувь и т.п.
|
Первая и вторая модели описывают тенденцию возрастания с монотонно убывающей скоростью.
Замечание Психофизика – наука, изучающая методы измерения субъективных ощущений человека, вызванных воздействием на его органы чувств различных стимуляторов (звука, света, электрического тока и так далее). Согласно основному закону психофизики: с увеличением интенсивности воздействия Х сила субъективных ощущений Y этого воздействия возрастает с монотонно убывающей скоростью.
Если рассматривать количество потребленного блага Х как интенсивность воздействия этого блага на человека, а субъективную полезность этого блага Y как уровень ощущений этого воздействия человеком, то закон убывающей предельной полезности есть одно и из проявлений общего закона психофизики в экономике.
Аналитическое описание закона психофизики при помощи степенной функции (1) называют законом Стивенса, при помощи логарифмической функции (2) – законом Фехнера.
 2014-02-09
2014-02-09 429
429








