Необходимые и достаточные условия сходимости итерационных методов.
Теорема 3.1. Для того чтобы метод простой итерации сходился необходимо и достаточно чтобы все собственные значения матрицы B=E-D-1A были по модулю меньше единицы.
Доказательство. Пусть X ( k )→ X *. Тогда, как мы видели, X * есть решение системы и, следовательно,
X * - X ( k ) = B (X * - X ( k- 1)) =... = B (X * - X (0)),
откуда Bk (X * - X (0))→0. Так как это должно иметь место при любом векторе X (0), Необходимо, чтобы Bk →0, длячего, в свою очередь, необходимо, чтобы все собственные значения матрицы B были меньше единицы по модулю.
Достаточность условия непосредственно вытекает из формулы
X(k)=B(k)X(0)+(E+B+…+Bk-1)G,
т.к. Bk→0 и E+B+ …+ Bk → (E – B)-1= A -1,если все собственные значения матрицы B меньше единицы по модулю.
Так как условие теоремы 3.1 трудно проверяется, судить о сходимости процесса последовательных приближений лучше при помощи достаточных признаков, связанных непосредственно с элементами матрицы В. Некоторые достаточные признаки вытекают из теоремы 3.1
Теорема 3.2. Для того чтобы процесс последовательных приближений сходился, достаточно, чтобы какая-либо норма матрицы В была меньше единицы.
Доказательство. Действительно, если ||B||<1, то все собственные значения матрицы В меньше единицы и потому на основании теоремы 1 процесс последовательных приближений сходится.
Если выполняется одно из условий:
I. 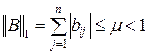 при
при 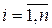 (3.1)
(3.1)
II. 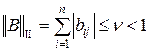 при
при 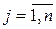 (3.2)
(3.2)
Ш. 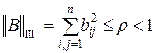 , (3.3)
, (3.3)
то процесс последовательных приближений сходится. Это равносильно преобладанию диагональных элементов в исходной матрице 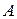 .
.
Дадим теперь оценки быстроты сходимости процесса последовательных приближений в терминах нормы. При этом выбор нормы векторов совершенно безразличен, но норма матриц должна быть согласована с выбранной нормой векторов.
Теорема 3.3. Если ||B||< 1, то
||X*-X(k)||≤||B||k||X(0)||+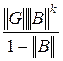 . (3.4)
. (3.4)
Доказательство. Имеем ||X*-X(k)||=||(E-B)-1G-(E+B+…+Bk-1)G-BkX(0)||≤
≤||(E-B)-1G -(E+B+…+Bk-1)G||+||BkX(0)||≤||(E-B)-1G-(E+B+…+Bk-1)G||+||Bk|X(0)||≤
≤||B||k||X(0)||+ 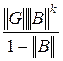 .
.
Часто бывает важно сравнить точность двух последовательных приближений, т.e. сравнить величины ||X*-X(k)|| и ||X*-Xk-1||. Taкое сравнение можно проводить наосновании следующей теоремы.
Теорема 3.4 ||X*-X(k)||≤||B|| ||X*-Xk-1||.
Доказательство. Действительно, из равенств
X*=BX*+G, Xk=BX (k-1)+G
следует, что
X*-X(k)=B(X*-X(k-1)).
Отсюда
||X*-X(k)||=||B(X*-X(k-1))|| ≤||B|| ||X*-X (k-1)||.
 2014-02-24
2014-02-24 7032
7032
