В||-||А. Назовем норму канонической, если дополнительно выполнены условия: д) если А = [аij], то |aij| < ||А||, причем для скалярной матрицы A = [a11] имеем ||А|| = |a11|; e) из неравенства |А| < |В| (A и B — матрицы) следует нepaвенство ||А|| < ||В||. B частности, ||А|| = || | А | ||. B дальнейшем для матрицы А = [aij] произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы: 1) ||А||m = |aij| (m - норма); 2) ||А||l = |aij| (l - норма); 3) ||А||k = (k - норма). В частности, для вектора эти нормы имеют следующие значения: (абсолютная величина вектора). Если компоненты вектора действительны, то имеем просто: Пусть имеется последовательность матриц Ak=[aij(k)] (k = 1, 2, …) (1.1) одного и того же типа m×n (i = 1, 2,..., m; j = 1, 2,..., n). Под пределом последовательности матриц Ak понимается матрица (1.2) Последовательность матриц, имеющая предел, называется сходящейся. Лемма 1.1. Для сходимости последовательности матриц Ak (k=1, 2,...) к матрице A нeoбходимо и достаточно, чmoбы при,(1.3) гдe ||А|| — любая каноническая норма матрицы A. При этом Действительно, если Ak→A=[aij], то |aij-aij(k)|<εпри k>N (ε). Отсюда |A-Ak|<εI где I — матрица типа m ×n, все элементы которой равны единице. B силу свойств ноpмы имеем: |A-Ak|≤ε||I|| при k>N(ε), следовательно, (1.4) Обратно, пусть выполнено условие (1.3). Тогда при k>N(ε) имеем: |aij-aij(k)|≤||A-Ak||<ε и, следовательно, т.е. Кроме того, если Ak→A, то имеем: | ||A||-||Ak|| |≤||A-Ak||→0 при k→∞. Поэтому . Следствие. Последовательность Ak→0 приk→∞ тогда и только тогда, когда. Пользуясь понятием предела матрицы, можно ввести в рассмотрение матричные ряды , (1.5) где Ак — матрицы одного и того же типа. Если предел (1.5) существует, то матричный ряд называется сходящимся, и матрица, полученная в пределе, называется суммой этого ряда. Если предела (1.5) не существует, то матричный ряд называется расходящимся и ему не приписывается никакой суммы.
Теорема 1.1. Если матричный ряд (1.5) сходится, то 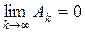 .
.
Доказательство. Пусть 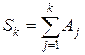 . Если ряд (1.5) сходится, то существует конечный предел
. Если ряд (1.5) сходится, то существует конечный предел 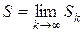 . Имеем: Ak=Sk-Sk-1,откуда
. Имеем: Ak=Sk-Sk-1,откуда
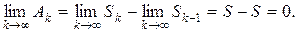
Матричный ряд (1.5) называется абсолютно сходящимся, если сходится ряд 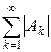 .
.
Теорема 1.2. Если ||A|| —любая каноническая норма, а числовой ряд 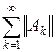 сходится, то матричный ряд (1.5) также сходится и притом абсолютно.
сходится, то матричный ряд (1.5) также сходится и притом абсолютно.
Теорема 1.3. Для того чтобы Am→0, необходимо а достаточно, чтобы все собственные значения матрицы А были по модулю меньше единицы.
 2014-02-24
2014-02-24 2345
2345








