Обусловленность матриц

Рассмотрим вопрос об устойчивости решения относительно изменения элементов матрицы.

Теоретическое решение системы 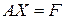дается формулой ,

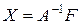где 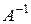- матрица, обратная к 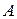. Обратную матрицу называют устойчивой, если малым изменениям в элементах матрицы соответствуют малые изменения в элементах обратной матрицы. Очевидно, что необходимым условием устойчивости обратной матрицы является то, чтобы определитель матрицы не был бы близок к нулю. Но это условие не является достаточным. В качестве меры близости к вырожденности матрицы 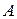рассматривают числа обусловленности:

,

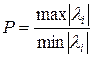где 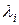- собственное значение матрицы 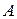; и .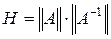

Матрицу называют плохо обусловленной, если соответствующая ей обратная матрица неустойчива.

Чем больше числа обусловленности, тем хуже обусловленность матрицы.

На практике этим определением обусловленности воспользоваться достаточно трудно, т.к. это связано с нахождением обратной матрицы и собственных значений матрицы. Поэтому обычно ограничиваются проверкой условия 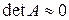. Для этого систему нормируют, т.е. 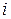-е уравнение системы делят на величину 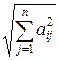, а затем определитель полученной матрицы сравнивают с единицей. Малость указанного определителя по сравнению с единицей является признаком плохой обусловленности системы.