2014-02-24
1658
Метод простой итерации.
Рассмотрим систему уравнений
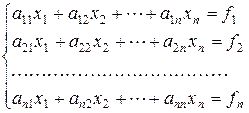(2.1)
Разделим каждое уравнение системы (2.1) на диагональный элемент. Получим систему
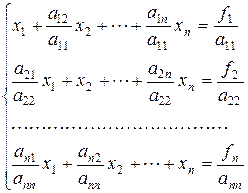
или в матричной форме
X=BX+G, (2.2)
где
, 
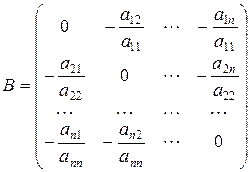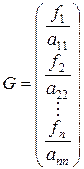(2.3)
Данное преобразование системы (2.1) в систему (2.2) равносильно умножению системы (2.1) слева на матрицу
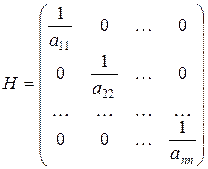
Таким образом, H=D-1,
где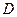 
- диагональная матрица [a11,…,ann].
Выберем начальное приближение X(0)=G. Строим последовательные приближения по формулам
X(k)=BX(k-1)+G, (2.4)
k =1,2,3,… или в развернутом виде
.
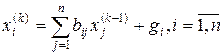Метод Зейделя.
Пусть система уравнений AX=F представлена в виде X=BX+G, где
B=E-A G=F.
Метод Зейделя похож на метод простой итерации с той лишь разницей, что при вычислении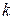 
-го приближения для 
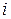-й компоненты учитываются вычисленные уже ранее 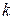-е приближения для компонент x1(k),…,xi-1(k).
Вычисление последовательных приближений ведется по формулам
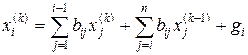(2.5)
Установим связь между методом Зейделя и методом простой итерации. Для этого матрицу В представим в виде суммы двух матриц: B=H+F, где
; 
.
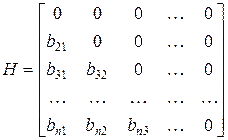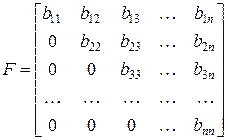Правило Зейделя в матричной форме перепишется в виде:
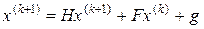или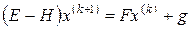 
; 
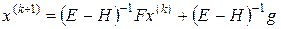, т.е. метод Зейделя эквивалентен методу простой итерации с матрицей (E-H)-1F.
