Пусть матрица 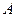 положительно определена. Тогда система AX=F всегда может быть подготовлена к виду, в котором метод последовательных приближений будет сходящимся. Подготовка состоит в переходе от данной системы AX=F к равносильной системе HAX=HF, где H- некоторая неособенная матрица, которая выбирается так, чтобы матрица HA была бы близка к единичной.
положительно определена. Тогда система AX=F всегда может быть подготовлена к виду, в котором метод последовательных приближений будет сходящимся. Подготовка состоит в переходе от данной системы AX=F к равносильной системе HAX=HF, где H- некоторая неособенная матрица, которая выбирается так, чтобы матрица HA была бы близка к единичной.
Положим
H=2E/μ, (3.5)
где μ – некоторая норма матрицы 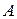 . Тогда система уравнений преобразуется к виду
. Тогда система уравнений преобразуется к виду
X=(E-2A/μ)X+2F/μ=BX+G. (3.6)
Собственные значения матрицы
B=(E-2A/μ)
будут заключены в открытом интервале (-1,1), в силу того собственные значения положительно определенной матрицы A находятся в интервале (0;μ). Следовательно, метод последовательных приближений для системы (3.6) будет сходящимся.
Исходя из полученной аналогии методов Зейделя и простой итерации, можно сформулировать следующий признак сходимости метода Зейделя: для того чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все собственные значения матрицы (E-H)-1F по модулю были меньше единицы. Другими словами, чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все корни уравнения |F+λH-λE|=0 по модулю были меньше единицы, т.к.
|(E-H)-1F-λE|=|(E-H)-1(E-H)[(E-H)-1F-λE]|=|(E-H)-1||F+λH-λE|=|F+λH-λE|=0.
Сформулируем достаточный признак сходимости: для того, чтобы метод Зейделя сходился, достаточно, чтобы выполнилось одно из условий:
1) 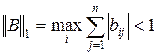 ;
;
2) 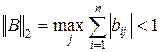 ;
;
3) 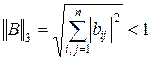 .
.
 2014-02-24
2014-02-24 1249
1249








