Изложим метод, позволяющий вычислять наибольшее по модулю собственное значение матрицы и принадлежащий ему собственный вектор при помощи вычисления последовательности итераций произвольного вектора. Излагаемый метод называется степенным и является простейшим итерационным процессом для решения частичной проблемы собственных значений. Он применим для произвольной матрицы, хотя ход итерационного процесса существенно зависит от того, как входит наибольшее по модулю собственное значение матрицы в ее каноническую форму Жордана. В связи с этим приходится различать несколько возможных случаев.
Для упрощения изложения мы будем предполагать, что все собственные значения матрицы, кроме, может быть, наибольшего по модулю, имеют линейные элементарные делители. Будем также считать, что элементы исследуемых матриц вещественны.
Наибольшее по модулю собственное значение вещественное и простое. В этом случае наибольшему по модулю собственному значению соответствует один линейный элементарный делитель, так что в силу только что сформулированного соглашения, все элементарные делители матрицы линейны. Поэтому существует базис из собственных векторов U 1, U2,…,Un, принадлежащихсобственным значениям λ1, λ2,...,λn, расположенным в порядке убывания модулей, причем |λ1|>|λ2|, но среди остальных могут быть равные. Возьмем произвольный вектор Y0 и образуем последовательность его итераций матрицей A
AY0, A2Y0,…,AkY0,…
Напишем разложение вектора Y 0 по собственным векторам
Y0=a1U1+a2U2+…+anUn . (5.1)
Среди чисел ai некоторые могут равняться нулю. Предположим, однако, что a 1 ≠0.
Очевидно, что
AY0=a1λ1U1+a2λ2U2+…+anλnUn,
… … … (5.2)
AkY0=a1λ1kU1+a2λ2kU2+…+anλnk Un.
Обозначим AkY0=Yk=(y1k,y2k,…,ynk)´ ивыясним структуру компонент вектора Yk. Пусть
U1=(u11, u21,…, un1)´, U2=(u12, u22,…, un2)´,…, U1=(u1n, u2n,…, unn)´.
Тогда из (5.2) получим
yik=a1ui1λ1k+ a2ui2λ2k+…+ anuinλnk.
Коэффициент при λ1k по крайней мере в однойизкомпонент не paвен нулю, так как a 1≠0 по предположению и вектор Ul не нулевой. Пусть yk (первый индекс опускаем) какая-либо из компонент вектора Yk, для которой коэффициент при λ1k отличен от нуля. Тогда
yk=c1λ1k+c2λ2k+…+cnλnk, (5.3)
причем коэффициент сi не зависит от индекса k и с1≠0.
Рассмотрим отношение компонент двух соседних итераций.
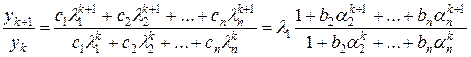 , (5.4)
, (5.4)
где
bi=ci/c1 ai= λi/λ1. (5.5)
Произведем деление и удерживая члены до порядка α22k и α 3k включительно, получим
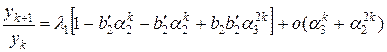 (5.6)
(5.6)
где
b2´=b2(1-α2), b´3=b3(1-α3) (5.7)
Отсюда мы видим, что если k достаточно велико, то
λ1≈yk+1/yk (5.8)
Так как обычно все компоненты вектора U1 отличны от нуля, то в качестве yk может быть взята, правило, любая компонента вектора Yk. таким образом, первое собственное значение приближенно равно отношению любых соответствующих компонент двух соседних достаточно высоких итераций произвольного вектора матрицей A.
При практическом выполнении итераций следует вычислять отношения yk+1/yk для нескольких компонент. Хорошее совпадение этих отношений yk+1/yk будет показывать, что в выражении (5.6) различие значений коэффициентов b2´,b1´ уже перестало играть заметную роль.
Быстрота сходимости процесса в рассматриваемом случае определяется величиной отношения λ2/λ1 и может быть медленной, если это отношение близко к единице.
Для того чтобы избежать роста компонент, иногда целесообразно при вычислении итераций тем или другим способом нормировать на каждом шагу получаемые векторы. Удобными нормировками являются деление вектора на его первую компоненту, или на наибольшую компоненту, или, наконец, нормировка к единичной длине.
При этом вместо последовательности Yk мы получим последовательность Ỹk=μkYk, где μk нормирующие множители, идля получения λ1 надо брать отношения компонент векторов AỸk и Ỹk.
Описанный процесс дает возможность определить также и все компоненты собственного вектора, принадлежащего наибольшему собственному числу. Именно, отношения компонент вектора Yk стремится к отношениям компонент этого собственного вектора.
Действительно, при a 1≠0
Yk=AkY0=λ1k[a1U1+a2(λ2/λ1)kU2+…+ an(λn/ λ1)kUn]=a1λ1k[U1+O(λ2/ λ1)k]. (5.9)
 2014-02-24
2014-02-24 2862
2862








