Разностные методы решения дифференциальных уравнений.
Рассмотрим линейное дифференциальное уравнение
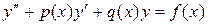 (19.1)
(19.1)
с двухточечными линейными краевыми условиями

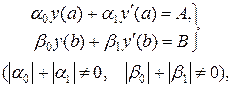 (19.2)
(19.2)
где р (х), q (х) и f(x) — непрерывны на отрезке [ а,b ].
Одним из наиболее простых методов решения этой краевой задачи является сведение ее к системе конечно-разностных уравнений. Для этого разобьем основной отрезок [а, b] на п paвных частей длины h (шаг), где
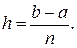
Точки разбиения имеют абсциссы xi = xo +ih (i = 0, 1, 2,..., n) x0 = а; хп = b.
Значения в точках деления xi искомой функции у=у(х) и ее производных у'=у'(x), у" =у" (х) обозначим соответственно через
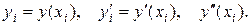
Введем также обозначения:
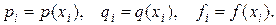
Заменяя производные правыми односторонними конечно-разностными отношениями, для внутренних точек xi отрезка [а, b] приближенно будем иметь
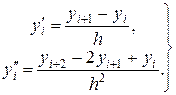 (19.3)
(19.3)
Для концевых точек х0 =а и хп = b полагаем
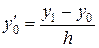 и
и 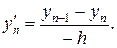 (19.4)
(19.4)
Используя формулы (19.3), дифференциальное уравнение (19.1) при x = xi (i=l, 2,..., п—1) приближенно можно заменить линейной системой уравнений
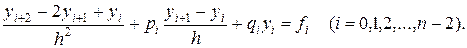 (19.5)
(19.5)
Кроме того, в силу формул (19.4) краевые условия (19.2) дополнительно дают еще два уравнения:
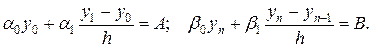 (19.6)
(19.6)
Таким образом, получена линейная система п+1 уравнений с n+1 неизвестными у0, у1,…,уп, представляющими собой значения искомой функции у=у(х) в точках х0, х1 , ...,хп. Решив эту систему, если это возможно, получим таблицу значений искомой фикции у.
Более точные формулы получаются, если воспользоваться симметричными конечно-разностными отношениями:
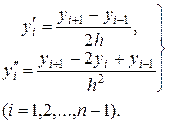 (19.7)
(19.7)
Для производных в концевых точках х0 = а и хп =b в общем случае по необходимости приходится пользоваться формулами (19.4). Отсюда получаем систему:
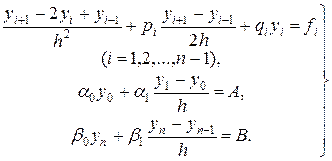 (19.8)
(19.8)
Метод прогонки.
При применении метода конечных разностей к краевым задачам для дифференциальных уравнений второго порядка получается «трехчленная система» линейных алгебраических уравнений, каждое и которых содержит три соседних неизвестных. Для решения такой системы разработан специальный метод, получивший название метода прогонка.
Рассмотрим линейное дифференциальное уравнение (19.1) с двухточечными линейными краевыми условиями (19.2) в предположении, что функции р (х), q(х), f(х) непрерывны на [а,b].
От дифференциального уравнения (19.1) обычным приемом перейдем к конечно-разностному уравнению. Для этого разобьем отрезок [а, b] на п равных частей с шагом 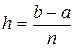 .
.
Полагая xi = xo +ih (i = 0, 1, 2,..., n) x0 = а; хп = b и вводя обозначения
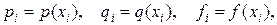
получаем при x = xi вместо дифференциального уравнения (19.1) следующее конечно-разностное уравнение:
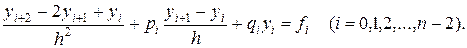
Отсюда после упрощения будем иметь
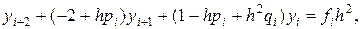 (19.9)
(19.9)
или, введя сокращенные обозначения
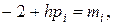
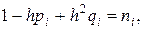
окончательно получим
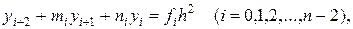 (19.10)
(19.10)
причем из краевых условий (19.2) имеем
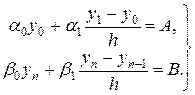 (19.11)
(19.11)
Линейная система (19.10), (19.11) состоит из п+1 уравнений относительно n+1 неизвестных у0, у1, у2,...,уп. Эту систему можно решить обычным способом. Однако укажем другой, более короткий путь. Разрешая уравнение (19.10) относительно yi + 1, находим
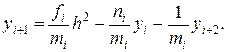 (19.12)
(19.12)
Предположим, что с помощью полной системы (19.10) из уравнения исключен член, содержащий уi. Тогда уравнение (19.12) может быть записано в виде
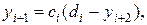 (19.13)
(19.13)
где коэффициенты сi, di подлежат определению. Найдем формулы для этих коэффициентов. При i = 0 из формулы (19.12) и краевых условий (19.11) следует, что
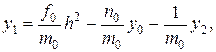
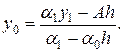
Исключая из этих двух уравнений у0, получим:
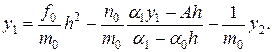
Разрешая последнее уравнение относительно у1, находим
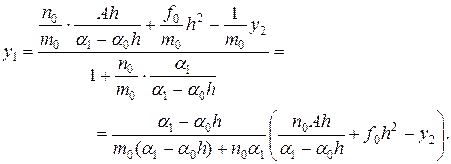 (19.14)
(19.14)
Но согласно формуле (19.13) имеем
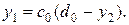 (19.15)
(19.15)
Отсюда, сравнивая формулы (19.14) и (19.15), находим
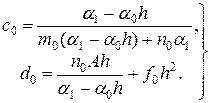 (19.16)
(19.16)
Пусть теперь i> 0 (i=1,2,,.., п — 2). Выражая yi по формуле (19.13), получим
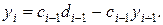
Подставляя это выражение в формулу (19.12), будем иметь
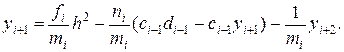
Разрешая полученное уравнение относительно уi+1, находим
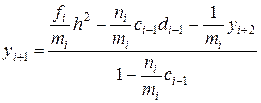
или
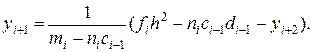 (19.17)
(19.17)
Отсюда, сравнивая формулы (19.13) и (19.17), получаем для коэффициентов ci и di рекуррентные формулы:
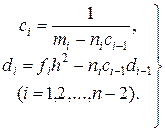 (19.18)
(19.18)
На основании формул (19.18), используя формулы (19.16) для с0 и d0, можно последовательно определить коэффициенты сi - и di (i = 1,2,..., п — 2) до сn- 2 и dn-2 включительно (прямой ход). Из формулы (19.13) при i = n — 2 и второго краевого условия (19.11) получаем
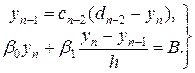
Решая эту систему двух уравнений относительно уп, будем иметь
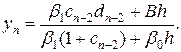 (19.19)
(19.19)
Теперь, используя формулу (19.13) и первое краевое условие (19.11), мы можем последовательно найти yn-1, yn-2,.,., у0 (обратный ход):
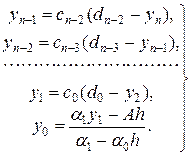 (19.20)
(19.20)
Для простейших краевых условий:
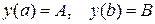
формулы для с0, d0, y0 и уп упрощаются. А именно, полагая
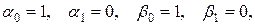
из формул (19.16), (19.19) и (19.20) будем иметь
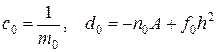 (19.21)
(19.21)
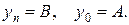 (19.22)
(19.22)
 2014-02-24
2014-02-24 3928
3928
