Лабораторная работа №1.
Требования к оформлению отчета о выполнении лабораторной работы
ЛАБОРАТОРНЫЕ РАБОТЫ
В отчет о выполнении лабораторной работы необходимо включить следующие пункты:
1. Тема лабораторной работы.
2.Постановка задачи и вариант задания.
3. Математическое описание метода решения поставленной задачи.
4. Листинг программы.
5. Результаты выполнения программы.
6. Анализ результатов и выводы.
Цель работы – решение системы уравнений одним из итерационных методов.
Теоретическая часть.
1) Метод простой итерации.
Рассмотрим систему уравнений
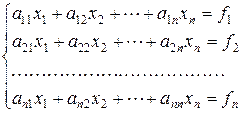 (1.1)
(1.1)
Разделим каждое уравнение системы (1.1) на диагональный элемент. Получим систему
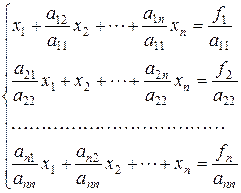
или в матричной форме
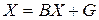 , (1.2)
, (1.2)
где
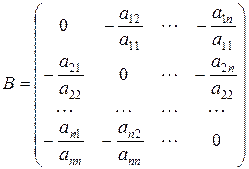 ,
, 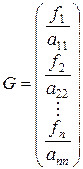 (1.3)
(1.3)
Данное преобразование системы (1.1) в систему (1.2) равносильно умножению системы (1.1) слева на матрицу
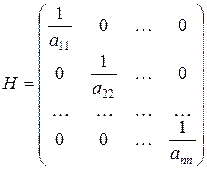
Таким образом, 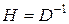 ,
,
где 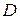 - диагональная матрица
- диагональная матрица 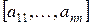 .
.
Выберем начальное приближение 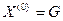 . Строим последовательные приближения по формулам
. Строим последовательные приближения по формулам
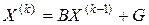 , (1.4)
, (1.4)
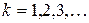 или в развернутом виде
или в развернутом виде
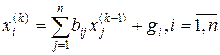
Необходимое и достаточное условие сходимости процесса простой итерации состоит в том, что все собственные значения матрицы 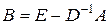 были по модулю меньше единицы. Укажем достаточные признаки сходимости процесса последовательных приближений:
были по модулю меньше единицы. Укажем достаточные признаки сходимости процесса последовательных приближений:
Если выполняется одно из условий:
I. 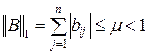 при
при 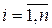
II. 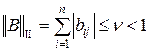 при
при 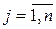
Ш. 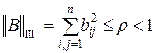 ,
,
то процесс последовательных приближений сходится.
Это равносильно преобладанию диагональных элементов в исходной матрице 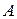 .
.
2) Метод Зейделя.
Пусть система уравнений 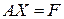 представлена в виде
представлена в виде
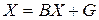 , (1.5)
, (1.5)
где 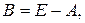
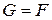 .
.
Метод Зейделя похож на метод простой итерации с той лишь разницей, что при вычислении 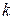 -го приближения для
-го приближения для 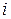 -й компоненты учитываются вычисленные уже ранее
-й компоненты учитываются вычисленные уже ранее 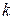 -е приближения для компонент
-е приближения для компонент 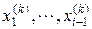 .
.
Вычисление последовательных приближений ведется по формулам
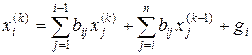 (1.6)
(1.6)
Рассмотрим вопрос об устойчивости решения относительно изменения элементов матрицы.
Теоретическое решение системы 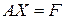 дается формулой
дается формулой 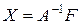 ,
,
где 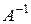 - матрица, обратная к
- матрица, обратная к 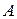 . Обратную матрицу называют устойчивой, если малым изменениям в элементах матрицы соответствуют малые изменения в элементах обратной матрицы. Очевидно, что необходимым условием устойчивости обратной матрицы является то, чтобы определитель матрицы не был бы близок к нулю. Но это условие не является достаточным. В качестве меры близости к вырожденности матрицы
. Обратную матрицу называют устойчивой, если малым изменениям в элементах матрицы соответствуют малые изменения в элементах обратной матрицы. Очевидно, что необходимым условием устойчивости обратной матрицы является то, чтобы определитель матрицы не был бы близок к нулю. Но это условие не является достаточным. В качестве меры близости к вырожденности матрицы 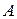 рассматривают числа обусловленности:
рассматривают числа обусловленности:
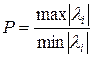 ,
,
где 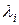 - собственное значение матрицы
- собственное значение матрицы 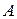 ; и
; и 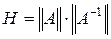 .
.
Матрицу называют плохо обусловленной, если соответствующая ей обратная матрица неустойчива.
Чем больше числа обусловленности, тем хуже обусловленность матрицы.
На практике этим определением обусловленности воспользоваться достаточно трудно, т.к. это связано с нахождением обратной матрицы и собственных значений матрицы. Поэтому обычно ограничиваются проверкой условия 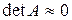 . Для этого систему нормируют, т.е.
. Для этого систему нормируют, т.е. 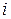 -е уравнение системы делят на величину
-е уравнение системы делят на величину 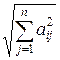 , а затем определитель полученной матрицы сравнивают с единицей. Малость указанного определителя по сравнению с единицей является признаком плохой обусловленности системы.
, а затем определитель полученной матрицы сравнивают с единицей. Малость указанного определителя по сравнению с единицей является признаком плохой обусловленности системы.
Подготовка системы уравнений к виду,
удобному для применения метода
последовательных приближений.
Пусть матрица 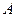 положительно определена. (Этого можно всегда добиться путем умножения матричного уравнения слева на транспонированную матрицу AТ. Тогда система
положительно определена. (Этого можно всегда добиться путем умножения матричного уравнения слева на транспонированную матрицу AТ. Тогда система 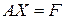 всегда может быть подготовлена к виду, в котором метод последовательных приближений будет сходящимся. Подготовка состоит в переходе от данной системы
всегда может быть подготовлена к виду, в котором метод последовательных приближений будет сходящимся. Подготовка состоит в переходе от данной системы 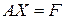 к равносильной системе
к равносильной системе 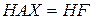 ,
,
где 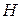 - некоторая неособенная матрица, которая выбирается так, чтобы матрица
- некоторая неособенная матрица, которая выбирается так, чтобы матрица 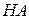 была бы близка к единичной.
была бы близка к единичной.
Положим
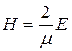 , (1.7)
, (1.7)
где 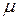 - норма матрицы
- норма матрицы 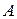 . Тогда система уравнений преобразуется к виду
. Тогда система уравнений преобразуется к виду
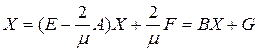 . (1.8)
. (1.8)
Собственные значения матрицы
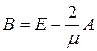
будут заключены в открытом интервале (-1,1), в силу того собственные значения положительно определенной матрицы 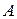 находятся в интервале
находятся в интервале 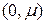 . Следовательно, метод последовательных приближений для системы (1.8) будет сходящимся.
. Следовательно, метод последовательных приближений для системы (1.8) будет сходящимся.
Порядок выполнения работы.
1. Изучить теоретическую часть.
2. Написать программу решения системы одним из указанных методов. Отладить программу на модельной задаче.
3. Определить три нормы матрицы.
4. Вычислить нормированный определитель матрицы.
5. Найти решение системы с заданной точностью. Для этого выход из цикла, осуществляющего итерационный процесс, производить, как только норма соответствующего вектора невязки 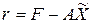 станет меньше наперед заданной точности ε.
станет меньше наперед заданной точности ε.
Выход из цикла можно также осуществлять, как только норма разности между векторами решений, полученных на данном шаге и на предыдущем станет меньше заданной погрешности.
6. Исследовать скорость сходимости метода в зависимости от числа итерации.
7. Сделать выводы о точности метода и быстроте его сходимости, а также об устойчивости матрицы исходя из величины его нормированного определителя.
Варианты заданий.
1) 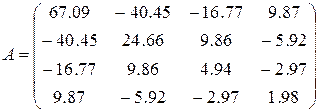 ,
, 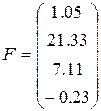
2) 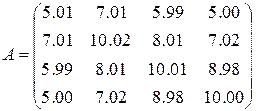 ,
, 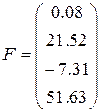
3) 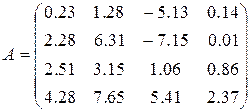 ,
, 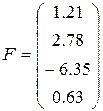
4) 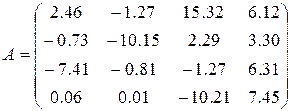 ,
, 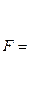
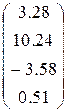
5) 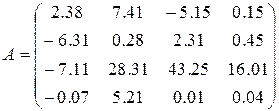 ,
, 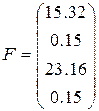
6) 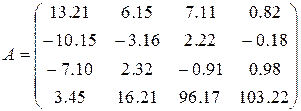 ,
, 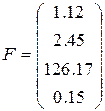
7) 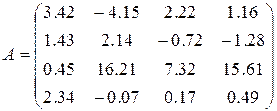 ,
, 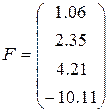
8) 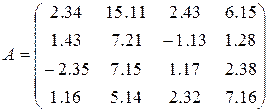 ,
, 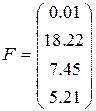
9) 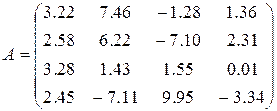 ,
, 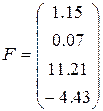
10) 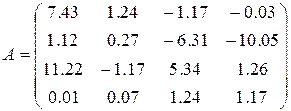 ,
, 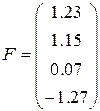
11) 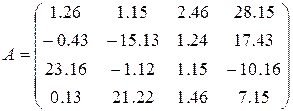 ,
, 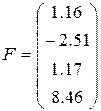
12)  ,
, 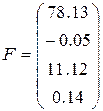
13) 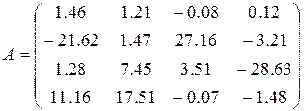 ,
, 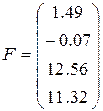
14) 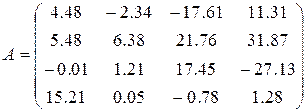 ,
, 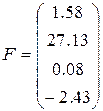
15) 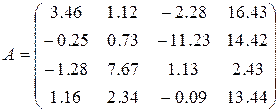 ,
, 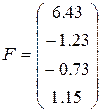
16) 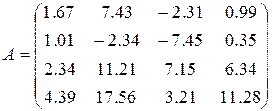 ,
, 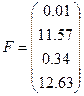
17) 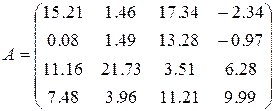 ,
, 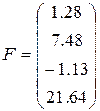
18) 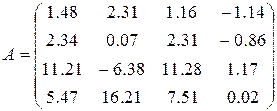 ,
, 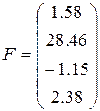
19) 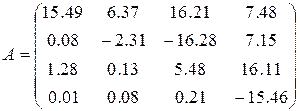 ,
, 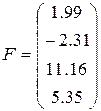
20) 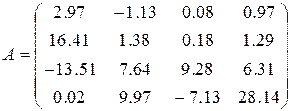 ,
, 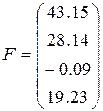
21) 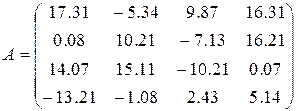 ,
, 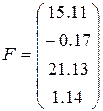
22) 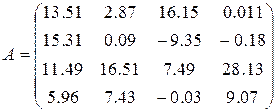 ,
, 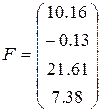
23) 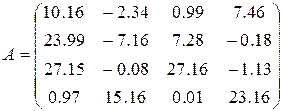 ,
, 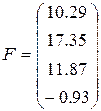
24) 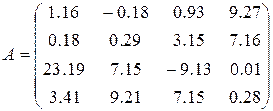 ,
, 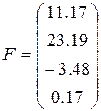
25) 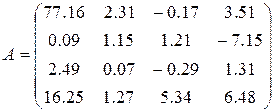 ,
,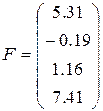
 2014-02-24
2014-02-24 681
681







