Преобразование Фурье. Пусть f(x)—периодическая функция с периодом l — может быть разложена в ряд Фурье

Пусть f(x) —периодическая функция с периодом l — может быть разложена в ряд Фурье

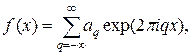(21.1)

причем

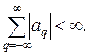(21.2)

Рассмотрим значения этой функции на сетке из точек 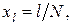где l, N – целые, N – фиксировано, и обозначим 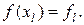Пусть 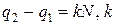- целое; тогда 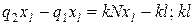- целое и, следовательно,

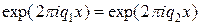(21.3)

в узлах сетки. Поэтому, если функция f(x) рассматривается лишь на сетке узлов х_l в соотношении (21.1) можно привести подобные члены

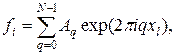(21.4)

где

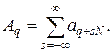
Если с самого начала была задана функция, определенная только на сетке, то на этой сетке ее можно также представить в форме (21.1). Действительно, такую функцию можно продолжить на всю прямую, доопределив ее между узлами сетки путем линейной интерполяции. Для непрерывной кусочно-дифференцируемой функции выполняется (21.2), и поэтому после приведения на сетке подобных членов получим (21.4). Определим скалярное произведение для функций на сетке:

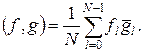
Множитель 1/ N введен для согласованности получаемых соотношений с непрерывным случаем: если f(x) и g(x) —непрерывные функции на [0, 1], то

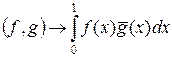
при N →∞.

Функци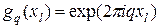и при 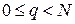образуют ортонормированную систему относительно так введенного скалярного произведения. Действительно,

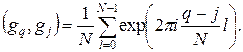
При 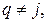суммируя геометрическую прогрессию, имеем

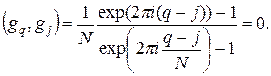
Поскольку 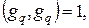то в итоге имеем

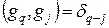при 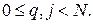(21.5)

Умножая (21.4) скалярно на 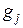, получим равенство

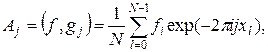(21.6)

очевидно,

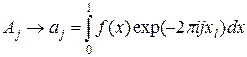
при 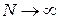и j фиксированном.

Однако это не означает, что

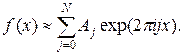
Посмотрим, почему это соотношение неверно. Пусть для простоты

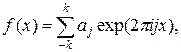
где 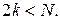Из (21.4) получаем представление для коэффициентов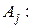

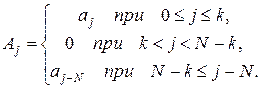
Таким образом, правая часть этого неверного приближенного равенства есть

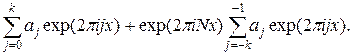
Она совпадает с f(x) в точках x_l, но далека от нее вне этих точек.

Заменой переменной суммирования 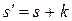в определении 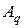убеждаемся, что 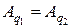, если 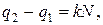где k – целое. Воспользовавшись равенством (21.3), перепишем (21.4) в виде

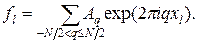(21.7)

Если f(x) – достаточно гладкая, то величины 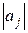с ростом j убывают быстро, и поэтому, 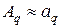при малых q; кроме того, тогда величины 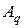и 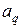малы при больших q. В итоге есть основание надеяться на справедливость приближенного равенства

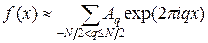(21.8)

во всех точках х.

Это приближенное равенство обращается в равенство в точках сетки. Способ аппроксимации функции правой частью (21.8) носит название тригонометрической интерполяции. Соотношение (21.7) называют конечным или дискретным рядом Фурье, а коэффициенты A_q — дискретными коэффициентами Фурье.

Быстрое преобразование Фурье. Осуществление прямого, и обратного дискретных преобразований Фурье

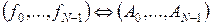
является составной частью решения многих задач. Непосредственное осуществление этих преобразований по формулам (21.4), (21.6) требует O(N²) арифметических операций. Рассмотрим вопрос о возможности сокращения этого числа операций; для определенности речь пойдет о вычислении коэффициентов A_q по заданным значениям функции. Идея построения алгоритмов быстрого преобразования Фурье опирается на то, что при N составном в слагаемых правой части (21.6) можно выделить группы, которые входят в выражения различных коэффициентов A_q.

Рассмотрим сначала случай 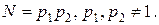Представим q, j, лежащие в пределах 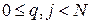в ви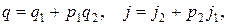де где 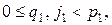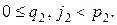Имеем цепочку соотношений

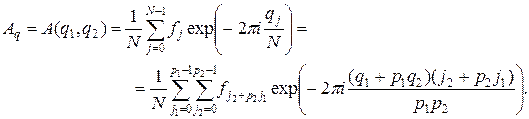
Из равенства

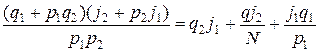
и предыдущего соотношения получим

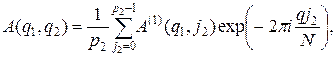
где

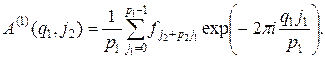
Непосредственное вычисление всех 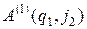требует 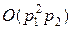арифметических операций, а последующее вычисление 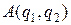требует еще 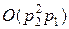операций. Следовательно, при 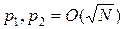общее число операций будет 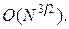Точно так же при 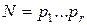строится алгоритм вычисления совокупности значений 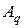, для которого общее число операций не превосходит 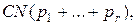здесь C – абсолютная постоянная. Выпишем соответствующие расчетные формулы для наиболее употребительного случая 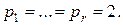Представим числа q, j в виде

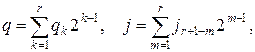
где 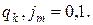Величину 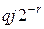можно представить в виде

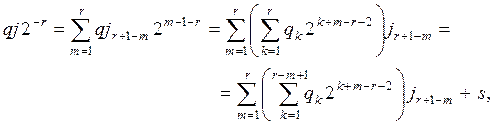
где s – целое, равное сумме всех слагаемых

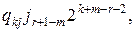
у которых 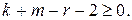Очевидно,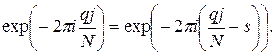

Поэтому

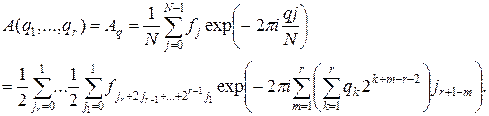
После перегруппировки слагаемых имеем

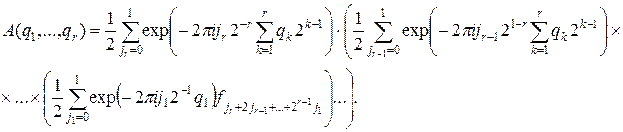
Это соотношение можно записать в виде последовательности реккурентных соотношений

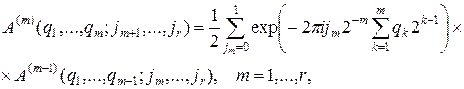
где

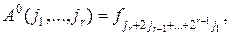
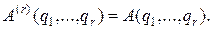
Задачи по курсу «Численные методы»

1.1 Привести системы к виду, удобному для итераций. Решить системы методом простой итерации с точностью до 10^-2. (Погрешность оценивать либо по вектору невязки, либо по модулю разности между двумя соседними итерациями.).

а)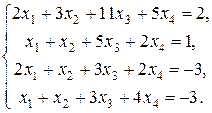 б)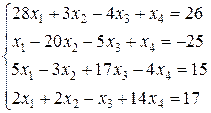

1.2 Привести системы к виду, удобному для итераций. Решить системы методом Зейделя с точностью до 10^-2. (Погрешность оценивать либо по вектору невязки, либо по модулю разности между двумя соседними итерациями.)

а)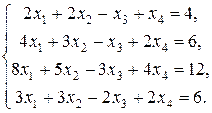 б)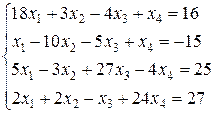

2.1 Определить наибольшее по модулю собственное значение и собственный вектор. (Наибольшее собственное значение – простое и вещественное)

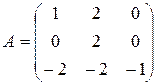
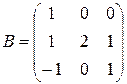
2.2 Определить наибольшее по модулю собственное значение и собственный вектор. (Наибольшие собственные значение – простые, вещественные и противоположные по знаку)

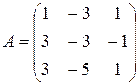
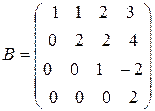
3.1 Найти приближенное положительное значение корня уравнения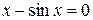методом Ньютона с точностью до .

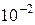3.2 Найти приближенное положительное значение корня уравнения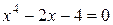методом Ньютона с точностью до .

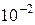3.3 Найти приближенное положительное значение корня уравнения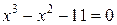методом половинного деления с точностью до .

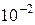3.4 Найти приближенное положительное значение корня уравнения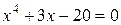методом половинного деления с точностью до .

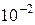3.5 Найти приближенное положительное значение корня уравнения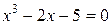методом Ньютона с точностью до .

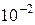3.6 Найти приближенное положительное значение корня уравнения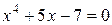методом половинного деления с точностью до .

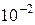4.1 Приближенно найти положительные решения систем уравнений

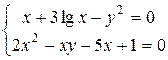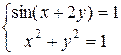а) б) в)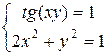

4.2 Методом Ньютона приближенно найти положительное решение системы уравнений

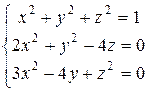
исходя из начального приближения .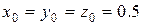

5.1 Построить конечные разности для функции P(x)=xⁿ, где n – целое положительное.

5.2 Составить горизонтальную и диагональную таблицы разностей функции y=4x⁴-5x³+2x²-3x+4 от начального значения x₀=0, приняв шаг h=1.

5.3 Составить горизонтальную и диагональную таблицы разностей функции y=2x³-4x²-6x+1 от начального значения x₀=0, приняв шаг h=1.

5.4 Приняв шаг h =0.05, построить на отрезке [3.5;3.6] интерполяционный многочлен Ньютона для функции y=e^x, заданной таблицей

x	3.50	3.55	3.60	3.65	3.70
y	33.115	34.813	36.598	38.475	40.447

5.5 Построить эмпирическую формулу для функции y, заданной таблицей

x
y	5.2	8.0	10.4	12.4	14.0	15.2

6.1 Для функции y=sinπx построить интерполяционный полином Лагранжа, выбрав узлы

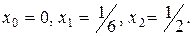
6.2 Дана таблица значений функции y=f(x)

x
y	2.5	2.6	2.7	2.8

Вычислить значение f( 323.5), приблизив функцию с помощью многочлена Лагранжа.

6.3Для функции y=cosπx построить интерполяционный полином Лагранжа, выбрав узлы

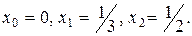
6.4 Дана таблица значений функции y=f(x)

x
y	4.0	4.3	4.5	4.2

Вычислить значение f (16.5), приблизив функцию с помощью многочлена Лагранжа.

7.1 Вычислить приближенное значение интеграла по формуле трапеций, приняв n =10. Оценить значение теоретической погрешности. Сравнить с точным значением интеграла. Вычисления проводить, сохраняя три знака после запятой.

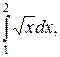
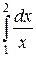
7.2 Вычислить приближенное значение интеграла по формуле Симпсона, приняв n=8. Оценить значение теоретической погрешности Сравнить с точным значением интеграла. Вычисления проводить, сохраняя шесть знаков после запятой.

,

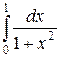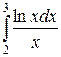
7.3 Вычислить приближенно по формуле Симпсона 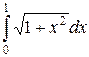с точностью до 0.001.

7.4 Вычислить приближенно по формуле Симпсона 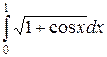с точностью до 0.001.

8.1 Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 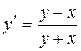при начальном условии y(0)=1; шаг h =0.1, ограничиться отысканием первых четырех значений y.

8.2 Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 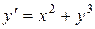при начальном условии y(0)=1; шаг h =0.1, ограничиться отысканием первых четырех значений y.

8.3 Методом Рунге-Кутта проинтегрировать уравнение 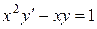при начальном условии y(1)= 0 в промежутке [1,2], шаг h =0.2.

8.4 Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 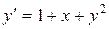при начальном условии y(0)=1; шаг h =0.1. ограничиться отысканием первых трех значений y.

8.5 Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 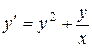при начальном условии y (2)=4; шаг h =0.1. ограничиться отысканием первых четырех значений y.

9.1 Графическим методом найти наибольшее значение функции 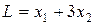при ограничениях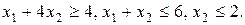

9.2 Минимизировать функцию L = x₁ — х₂ при ограничениях: 3≤x₁ + x₂ ≤7, 1 ≤х₂ ≤4, х₁ ≤4.

9.3 Найти наибольшее значение функции L = — x₁ +2x₂ при ограничениях: х₁ — 8 х₂ ≤10, х₁+ х₂≥1, х₁ — 5 х ₂ ≥—5, Зх₁ + 10х₂ ≤30.

9.4 Максимизировать линейную форму L = x₂ + x ₃ при ограничениях:

х₁-x₂ + x₃ =1, х₂ — 2x₃ +x₄ = 2.

9.5 Задана система ограничений: х₁ +х₂ +2х₃ — х₄ = 3, х₂ + 2х₄ = 1 и линейная форма L=5x₁ — x₃. Найти оптимальное решение, минимизирующее линейную форму.

9.6 Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия I вида расходуется 2 кг металла, а изделия II вида—4 кг. Составить план производства, обеспечивающий получение наибольшей прибыли от продажи изделий, если отпускная стоимость одного изделия I вида составляет 3 руб., а изделия II вида — 2 руб., причем изделий I вида требуется изготовить не более 40, а изделий II вида—не более 20.

9.7. Производственная мощность цеха сборки составляет 120 изделий типа А и 360 изделий типа В в сутки. Технический контроль пропускает в сутки 200 изделий того или другого типа (безразлично). Изделия типа А вчетверо дороже изделий типа В. Требуется спланировать выпуск готовой продукции так, чтобы предприятию была обеспечена наибольшая прибыль.