Одним из старейших методов решения дифференциальных уравнений является метод разложения в ряд Тейлора.
Пусть требуется найти на отрезке 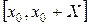 решение дифференциального уравнения (18.1) при начальном условии (18.2). f(x,y) аналитична в точке
решение дифференциального уравнения (18.1) при начальном условии (18.2). f(x,y) аналитична в точке 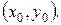 Дифференцируя (18.1) по x, имеем соотношения
Дифференцируя (18.1) по x, имеем соотношения
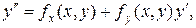
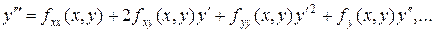
Подставляя 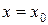 и
и 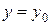 , получаем последовательно значения
, получаем последовательно значения
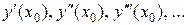
Таким образом, можно написать приближенное равенство

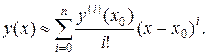 (18.5)
(18.5)
Если 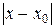 больше радиуса сходимости ряда
больше радиуса сходимости ряда
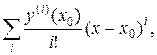
то погрешность (18.5) не стремится к нулю при n →∞. Иногда целесообразно поступить следующим образом.
Разобьем 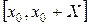 на отрезки
на отрезки
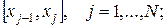
последовательно получаем приближения yj к значениям решения
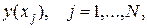
по следующему правилу: пусть значение yj уже найдено, вычисляем значения в точке xj производных 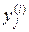 решения исходного дифференциального уравнения, проходящего через точку
решения исходного дифференциального уравнения, проходящего через точку 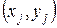 ; на отрезке
; на отрезке 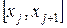 полагаем
полагаем
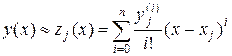 (18.6)
(18.6)
и, соответственно полагаем
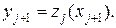 (18.7)
(18.7)
Методы Рунге-Кутта и Эйлера. В частном случае п = 1 расчетная формула (18.6) имеет вид
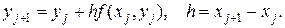 (18.8)
(18.8)
Этот метод называется методом Эйлера. Можно построить другой класс расчетных формул, к которому принадлежит метод Эйлера. Укажем сначала простейшие методы этого класса, получаемые из наглядных соображений. Пусть известно значение решения у(х) и требуется вычислить значение y(x+h). Рассмотрим равенство
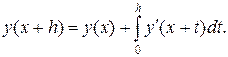 (18.9)
(18.9)
При замене интеграла в правой части на величину 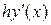 погрешность имеет порядок
погрешность имеет порядок 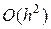 , т.е.
, т.е.
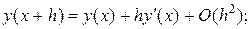
поскольку 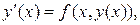 то отсюда имеем
то отсюда имеем
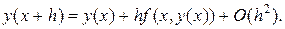
Отбрасывая член порядка 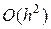 и обозначая
и обозначая 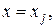
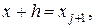 получим расчетную формулу Эйлера (18.8). Для получения более точной расчетной формулы нужно точнее аппроксимировать интеграл в правой части (18.9). Воспользовавшись формулой трапеций, получим
получим расчетную формулу Эйлера (18.8). Для получения более точной расчетной формулы нужно точнее аппроксимировать интеграл в правой части (18.9). Воспользовавшись формулой трапеций, получим
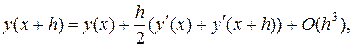
иначе,
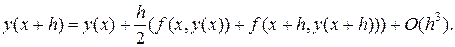 (18.10)
(18.10)
Соответствующая расчетная формула:
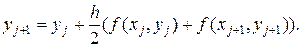 (18.11)
(18.11)
Обычно это уравнение неразрешимо явно относительно 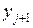 . Поэтому произведем дальнейшее преобразование алгоритма. Заменим
. Поэтому произведем дальнейшее преобразование алгоритма. Заменим 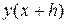 в правой части (18.10) на некоторую величину
в правой части (18.10) на некоторую величину
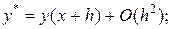 (18.12)
(18.12)
тогда правая часть изменится на величину
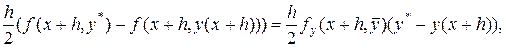
где 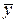 находится между
находится между 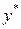 и
и 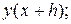 вследствие предположения (18.12) эта величина имеет порядок
вследствие предположения (18.12) эта величина имеет порядок 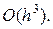 Таким образом, при условии (18.12)
Таким образом, при условии (18.12)
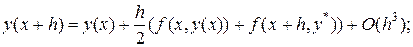
условию (18.12) удовлетворяет результат вычислений по расчетной формуле Эйлера
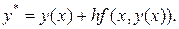
Последние соотношения определяют пару расчетных формул
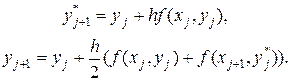 (18.13)
(18.13)
Построим другую пару формул с погрешностью на шаге такого же порядка. Интеграл в правой части (18.9) заменим по формуле прямоугольников:
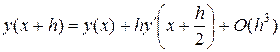
или, все равно, что
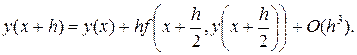
Если
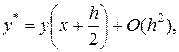
то, как и в предшествующем случае, имеем
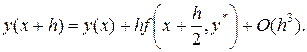
В качестве 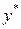 можно взять результат вычислений по формуле Эйлера с шагом
можно взять результат вычислений по формуле Эйлера с шагом 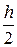 :
:
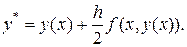
Этим соотношениям соответствует пара расчетных формул
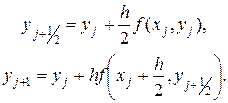 (18.14)
(18.14)
Полученные методы относятся к семейству методов Рунге-Кутта, имеющих следующий вид. В процессе вычислений фиксированы некоторые числа
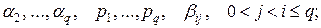
последовательно получаем
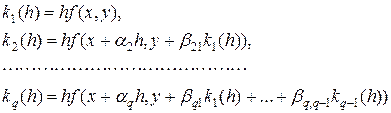
и полагаем
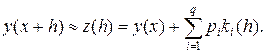
 2014-02-24
2014-02-24 1127
1127
