Метод последовательных приближений. Изложим этот метод применительно к дифференциальному уравнению первого порядка
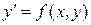 (18.1)
(18.1)
с начальным условием
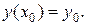 (18.2)
(18.2)
Предполагается, что в некоторой окрестности точки М0 (x0, у0) уравнение (18.1) удовлетворяет условиям теоремы существования и единственности решения.
Будем строить, искомое решение у=у(х) для значений х≥х0 Случай х≤х0 вполне аналогичен. Интегрируя правую и левую части уравнения (18.1) в пределах от х0 до х, получим
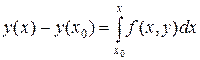
или, в силу начального условия (18.2), будем иметь
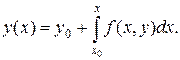 (18.3)
(18.3)
Так как искомая функция у=у(х) находятся под знаком интеграла, то уравнение (18.3) является интегральным. Очевидно, решение интегрального уравнения (18.3) удовлетворяет дифференциальному уравнению (18.1) и начальному условию (18.2).
Для нахождения этого решения применим метод последовательных приближений. Заменяя в равенстве (18.3)неизвестную функцию у данным значением у0, получим первое приближение
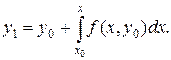
Далее, подставив в равенстве (18.3) вместо неизвестной функции у найденную функцию y1, будем иметь второе приближение
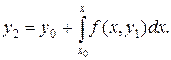
Вообще, все дальнейшие приближения строятся по формуле
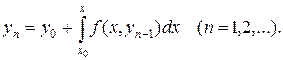 (18.4)
(18.4)
Геометрически последовательные приближения представляют собой кривые уп = уп(х) (n=1, 2,...), проходящие через общую точку M0(x0,y0).
Замечание. При методе последовательных приближений в качестве начального приближения у0, вообще говоря, можно выбирать любую функцию, достаточно близкую к точному решению у.
Например, иногда выгодно в качестве у0 брать конечный отрезок ряда Тейлора искомого решения.
Заметим, что при пользовании методом последовательных приближений аналитичность правой части дифференциального уравнения не обязательна, поэтому метод этот можно применять и в тех случаях, когда разложение решения дифференциального уравнения в степенной ряд невозможно.
Пример 18.1. Методом последовательных приближений найти приближенное решение дифференциального уравнения
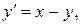
удовлетворяющее начальному условию
у(0)=1.
Решение. В качестве начального приближения возьмем у0 (х) = 1. Так как
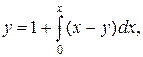
то будем иметь
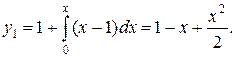
Аналогично
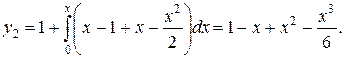
Подобным же образом получим
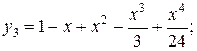
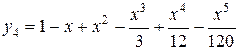
и т.д.
 2014-02-24
2014-02-24 2753
2753
