Метод разложение на множители
Решить уравнение cos2x+sinx cosx=1
cosx=1
Решение: cos2x+sinx cosx=1
cosx=1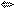 cos2x+sinx
cos2x+sinx cosx−cos2x−sin2x=0
cosx−cos2x−sin2x=0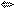 sinx
sinx cosx−sin2x=0
cosx−sin2x=0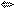 sinx
sinx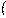 cosx−sinx
cosx−sinx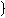 =0
=0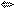
 sinx=0
sinx=0 cosx−sinx=0
cosx−sinx=0
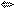
 sinx=0
sinx=0 tgx=1
tgx=1
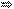
 x=
x= n
n n
n Z
Z x=
x= 4+
4+ k
k k
k Z
Z .
.
Решить уравнение 3sinx+4cosx=1
Решение: Используя формулы двойного угла и основное тригонометрическое тождество, приводим данное уравнение к половинному аргументу:3 2sinx2cosx2+4cos2x2−4sin2x2=sin2x2+cos2x2. После приведения подобных слагаемых имеем: 5sin2x2−6sinx2
2sinx2cosx2+4cos2x2−4sin2x2=sin2x2+cos2x2. После приведения подобных слагаемых имеем: 5sin2x2−6sinx2 cosx2−3cos2x2=0. Разделив однородное последнее уравнение на cos2x2
cosx2−3cos2x2=0. Разделив однородное последнее уравнение на cos2x2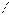 =0, получим 5tg2x2−6tgx2−3=0. Введем новую переменную tgx2=t, получим квадратное уравнение 5t2−6t−3=0, корнями которого являются числа t1
=0, получим 5tg2x2−6tgx2−3=0. Введем новую переменную tgx2=t, получим квадратное уравнение 5t2−6t−3=0, корнями которого являются числа t1 2=53
2=53
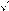 24 Таким образом tg2x1=53−2
24 Таким образом tg2x1=53−2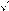 6иtg2x2=53+2
6иtg2x2=53+2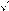 6. Общее решение можно записать так x1
6. Общее решение можно записать так x1 2=2arctg53
2=2arctg53 2
2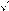 6+2
6+2 k
k k
k Z
Z
Замечание. Выражение cos2x2 обращается в нуль при x2= 2+
2+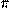 k
k k
k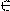 Z, т.е. при x=
Z, т.е. при x=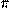 +2
+2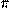 k
k k
k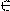 Z. Полученное нами решение уравнения не включает в себя данные числа.
Z. Полученное нами решение уравнения не включает в себя данные числа.
 2014-02-24
2014-02-24 958
958








