Случайные события. Возведение многочлена в степень

Возведение многочлена в степень

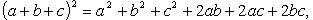
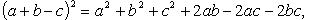
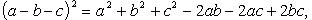
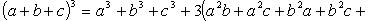
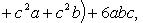
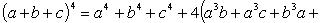
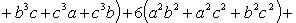
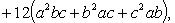
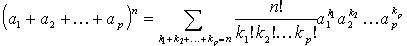
(сумммирование ведется по всем целым неотрицательным 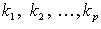, таким, что ).

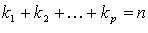Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Определение, основные формулы

Классическое определение вероятности

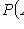
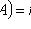
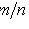
(m - число благоприятных исходов опыта; n - число всех его исходов)

Теорема сложения вероятностей несовместных событий

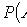
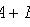
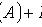
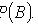
Теорема сложения вероятностей совместных событий

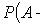
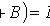
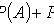
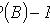
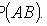
Теорема умножения вероятностей независимых событий

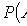
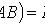
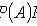
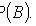
Теорема умножения вероятностей зависимых событий

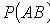
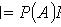
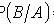
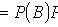
где 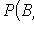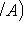- вероятность события B при условии, что произошло событие A.

Формула полной вероятности

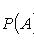
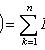
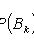
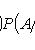
где 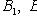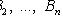- полная группа гипотез, т. е.

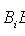
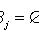
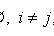
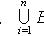
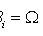
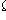
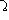( - достоверное событие).

Формула Бейеса

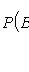
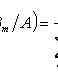
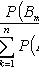
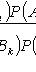
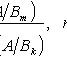
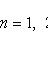
где 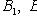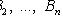- полная группа гипотез.

Повторение испытаний

Формула Бернулли

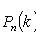
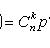
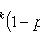
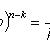
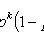
где 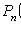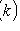- вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

Вероятность того, что при этом событие A:

1) наступит n раз: ;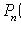

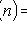
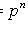2) не наступит ни разу: ;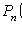

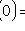
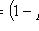
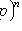3) наступит хотя бы один раз: ;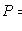

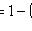
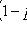
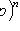4) наступит не более k раз: ;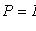

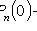
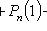
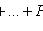
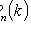5) наступит не менее k раз: .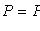

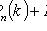
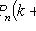
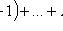
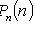Локальная теорема Лапласа

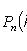
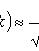
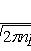
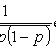
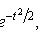
где 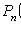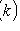вероятность появления события A ровно k раз при n независимых испытаниях p вероятность появления события A при каждом испытании

.

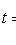
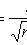
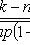
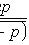Интегральная теорема Лапласа

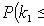
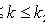
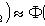
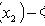
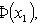
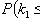
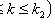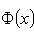
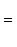
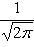
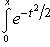
где - вероятность того, что в n независимых испытаниях событие A появится не менее k₁ и не более k₂ раз; 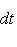- функция Лапласа; ; .

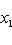
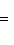
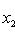
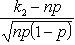Оценка отклонения относительной частоты от постоянной вероятности

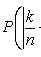
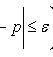
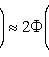
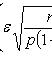
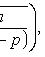
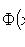
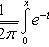
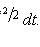
Наивероятнейшее число k₀ появления события A при n независимых испытаниях

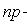
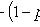
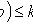
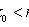
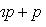
(n - число испытаний; p - вероятность появления события при одном испытании).