Выпуклые многогранники. Теорема Эйлера

В школьных учебниках геометрии многогранниками обычно называются тела, поверхности которых состоят из конечного числа многоугольников, назы­ваемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.

Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок.

На рисунке 1 приведены примеры выпуклых и невыпуклых многогранников.

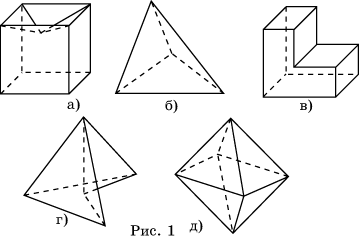
Рассмотрим некоторые свойства выпуклых многогранников.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

Доказательство. Пусть F - какая-нибудь грань многогранника M, и A, B – точки, принадлежащие грани F (рис. 2). Из условия вы­пуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоуголь­ника F, он будет целиком содержаться и в этом многоугольнике, т.е. F - выпуклый многоугольник.

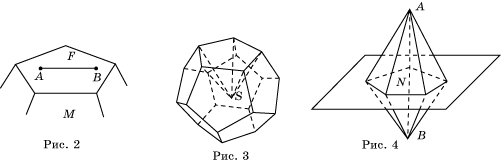
Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Доказательство. Пусть M - выпуклый многогранник. Возьмем ка­кую-нибудь внутреннюю точку S многогранника M, т.е. такую его точку, которая не принадлежит ни одной грани многогранника M. Соединим точку S с вершинами многогранника M отрезками (рис. 3). Заметим, что в силу вы­пуклости многогранника M, все эти отрезки содержатся в M. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранни­ка M. Эти пирамиды целиком содержатся в M, и все вместе составляют многогранник M.

Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.

Доказательство. Предположим противное, т.е. существуют точки A и B многогранника M, лежащие по разные стороны от плоскости некоторой его грани N (рис. 4). Рассмотрим пирамиды с вершинами в точках A, B, основаниями которых является грань N. В силу выпуклости многогранника, эти пирамиды целиком в нем содержатся. Это противоречит тому, что N является гранью многогранника M.

Для выпуклых многогранников имеет место свойство, связывающее число его вершин, ребер и граней, доказанное в 1752 году Леонардом Эйлером, и получившее название теоремы Эйлера.

Прежде чем его сформулировать рассмотрим известные нам многогранники и заполним следующую таб­лицу, в которой В - число вершин, Р - ребер и Г - граней данного мно­гогранника:

Название многогранника	В	Р	Г
Треугольная пирамида
Четырехугольная пирамида
Треугольная призма
Четырехугольная призма
n- угольная пирамида	n +1	2 n	n +1
n- угольная призма	2 n	3 n	n+2
n- угольная усеченная пирамида	2 n	3 n	n+2

Из этой таблицы непосредственно видно, что для всех выбранных мно­гогранников имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо не только для этих многогранников, но и для про­извольного выпуклого многогранника.

Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство

В - Р + Г = 2,

где В - число вершин, Р - число ребер и Г - число граней данного мно­гогранника.

Доказательство. Для доказательства этого равенства представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) од­ну из его граней и оставшуюся поверхность растянем на плоскости. Полу­чим многоугольник (образованный ребрами удаленной грани многогранника), разбитый на более мелкие многоугольники (образованные остальными гранями многогранника).

Заметим, что многоугольники можно деформировать, увеличивать, уменьшать или даже искривлять их стороны, лишь бы при этом не происходило разрывов сторон. Число вершин, ребер и граней при этом не изменится.

Докажем, что для полученного разбиения многоугольника на более мелкие многоугольники имеет место равенство

(*) В - Р + Г ' = 1,

где В – общее число вершин, Р – общее число ребер и Г ' – число многоугольников, входящих в разбиение. Ясно, что Г '= Г – 1, где Г – число граней данного мно­гогранника.

Докажем, что равенство (*) не изменится, если в каком-нибудь многоугольнике данного разбиения провести диагональ (рис. 5, а). Действитель­но,после проведения такой диагонали в новом разбиении будет В вершин, Р+1 ребер и количество многоугольников увеличится на единицу. Следовательно, имеем

В - (Р + 1) + (Г '+1) = В – Р + Г '.

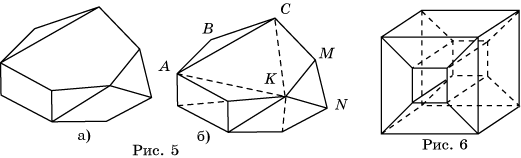
Пользуясь этим свойством, проведем диагонали, разбивающие входя­щие многоугольники на треугольники, и для полученного разбиения пока­жем выполнимость равенства (*) (рис. 5, б). Для этого будем последо­вательно убирать внешние ребра, уменьшая количество треугольников.

При этом возможны два случая:

а) для удаления треугольника ABC требуется снять два ребра, в на­шем случае AB и BC;

б) для удаления треугольника MKN требуется снять одно ребро, в нашем случае MN.

В обоих случаях равенство (*) не изменится. Например, в первом случае после удаления треугольника граф будет состоять из В – 1 вершин, Р – 2 ребер и Г ' – 1 многоугольника:

(В - 1) - (Р + 2) + (Г ' – 1) = В – Р + Г '.

Самостоятельно рассмотрите второй случай.

Таким образом, удаление одного треугольника не меняет равенство (*). Продолжая этот процесс удаления треугольников, в конце концов, мы придем к разбиению, состоящему из одного треугольника. Для такого раз­биения В = 3, Р = 3, Г ' = 1 и, следовательно, B – Р + Г ' = 1. Значит, равенство (*) имеет место и для исходного разбиения, откуда оконча­тельно получаем, что для данного разбиения многоугольника справедливо равенство (*). Таким образом, для исходного выпуклого многогранника справедливо равенство В - Р + Г = 2.

Пример многогранника, для которого не выполняется соотношение Эйлера, показан на рисунке 6. Этот многогранник имеет 16 вершин, 32 ребра и 16 граней. Таким образом, для этого многогранника выполняется равенство В – Р + Г = 0.

Используя соотношение Эйлера, докажем, следующее свойство выпуклых многогранников.

Свойство 4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.

Действительно, в каждой вершине многогранника сходится, по крайней мере, три ребра. Если количество вершин равно В и в каждой из них сходится три ребра, то общее число ребер будет больше или равно 3В: 2. Делить на два нужно потому, что при таком подсчете ребер мы каждое ребро посчитаем дважды – один раз, как ребро выходящее из одной его вершины, а второй раз, как ребро, выходящее из второй его вершины. Таким образом, для любого многогранника имеет место неравенство 3В 2Р.

Обозначим через Г _n число граней с n ребрами. Тогда Г = Г₃ + Г₄ + Г₅ + Г₆. Каждая треугольная грань имеет три ребра и число треугольных граней равно Г₃. Поэтому общее число ребер в треугольных гранях равно 3Г₃. Аналогично, общее число ребер в четырехугольных гранях равно 4Г₄ и т. д.

Поскольку каждое ребро многогранника содержится ровно в двух гранях, то при таком подсчете ребер, мы каждое ребро посчитаем дважды и, следовательно, будет иметь место равенство 2Р = 3Г₃ + 4Г₄ + 5Г₅ + 6Г₆.

Воспользуемся равенством 6В – 6Р + 6Г = 12, получающимся умножением обеих частей сооотношения Эйлера на 6. По доказанному выше, имеет место неравенство 6В 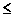4Р и, следовательно, неравенство 6Г – 2Р 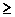12. С другой стороны, 6Г = 6Г₃ + 6Г₄ + 6Г₅ + 6Г₆, 2Р = 3Г₃ + 4Г₄ + 5Г₅ + 6Г₆. Подставляя эти выражения в неравенство, получим неравенство 3Г₃ + 2Г₄ + Г₅ + 0Г₆ – Г₇ – 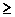12. В левой части, начиная с Г₇ стоят отрицательные числа. Поэтому для того, чтобы вся сумма была больше или равна 12 нужно, чтобы хотя бы одно из чисел Г₃ или Г₄ или Г₅ было отлично от нуля, т.е. в многограннике существовала грань с соответствующим числом ребер.

Правильные многогранники

Выпуклый многогранник называется правильным, если его гранями яв­ляются равные правильные многоугольники, и все многогранные углы равны.

Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 7). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот мно­гогранник называется также правильным тетраэдром, или просто тетраэдром, что в переводе с греческого языка означает четырехгранник.

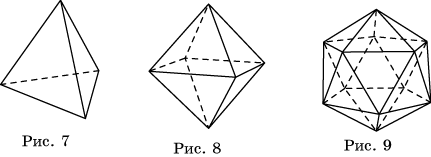
Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 8. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.

Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 9. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.

Заметим, что поскольку в вершинах выпуклого многогранника не мо­жет сходиться более пяти правильныхтреугольников, то другихправиль­ных многогранников, гранями которых являются правильные треугольники, не существует.

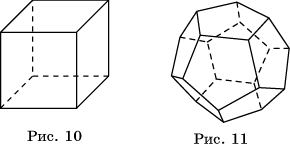
Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 10), других пра­вильных многогранников, у которых гранями являются квадраты не сущест­вует. Куб имеет шесть граней и поэтому называется также гексаэдром.

Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 11. Его по­верхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.

Рассмотрим понятие правильного многогранника с точки зрения топо­логии науки, изучающей свойсва фигур, не зависящих от различных дефор­маций без разрывов. С этой точки зрения, например, все треугольники эквивалентны, так как один треугольник всегда может быть получен из любого другого соответствующим сжатием или растяжением сторон. Вообще все многоугольники с одинаковым числом сторон эквивалентны потой же причине.

Как в такой ситуации определить понятие топологически правильного многогранника? Иначе говоря, какие свойства в определении правильного многогранника являются топологически устойчивыми и их следует оста­вить, а какие не являются топологически устойчивыми и их следует отб­росить.

В определении правильного многогранника количество сторон и коли­чество граней являются топологически устойчивыми, т.е. не меняющимися при непрерывных деформациях. Правильность же многоугольников не явля­етсятопологически устойчивым свойством. Таким образом, мы приходим к следующему определению.

Выпуклый многогранник называется топологически правильным, если его гранями являются многоугольники с одним и тем же числом сторон и в каждой вершине сходится одинаковое число граней.

Два многогранника называются топологически эквивалентными, если один из другого можно получить непрерывной деформацией.

Например, все треугольные пирамиды являются топологически пра­вильными многогранниками, эквивалентнымимежду собой. Все параллелепи­педы также являются эквивалентными между собой топологически правиль­ными многогранниками.Не являются топологи­чески правильными многогранниками, например, четырехугольныепирамиды.

Выясним вопрос о том, сколько существует не эквивалентных между собой топологически правильных многогранников.

Как мы знаем, существует пять правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр и додекаэдр. Казалось бы, топологичес­ки правильных многогранников должно быть гораздо больше. Однако оказы­вается, что никаких других топологически правильных многогранников, не эквивалентных уже известным правильным, не существует.

Для доказательства этого воспользуемся теоремой Эйлера. Пусть дан топологически правильный многогранник, гранями которого являются n - угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трех. Обозначим, как и раньше, В - число вершин, Р - число ребер и Г - число граней этого многогранника. Тогда

n Г = 2P; Г =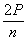; m B = 2P; В = .

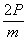По теореме Эйлера, В - Р + Г = 2 и, следовательно,

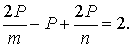
Откуда Р = .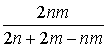

Из полученного равенства, в частности, следует, что должно выполняться неравенство 2 n + 2 m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2) < 4.

Найдем всевозможные значения n и m, удовлетворяющие найденному неравенству, и заполним следующую таблицу

N m
	B=4, Р=6, Г=4 тетраэдр	В=6, Р=12, Г=8 октаэдр	В=12, Р=30, Г=20 икосаэдр
	В=8, Р=12, Г=4 куб	Не существует	Не существует
	В=20, Р=30, Г=12 додекаэдр	Не существует	Не существует

Например, значения n = 3, m = 3 удовлетворяют неравенству (n – 2)(m – 2) < 4. Вычисляя значения Р, В и Г по приведенным выше формулам, получим Р = 6, В = 4, Г = 4.

Значения n = 4, m = 4 не удовлетворяют неравенству (n – 2)(m – 2) < 4 и, следовательно, соответствующего многогранника не существует.

Самостоятельно проверьте остальные случаи.

Из этой таблицы следует, что возможными топологически правильными многогранниками являются только правильные многогранники, перечислен­ные выше, и многогранники, им эквивалентные.

Призма — это многогранник, у которого две грани (основания призмы) — равные многоугольники с соотвественно параллельными сторонами. Остальные грани — параллелограммы, плоскости которых параллельны одной прямой.

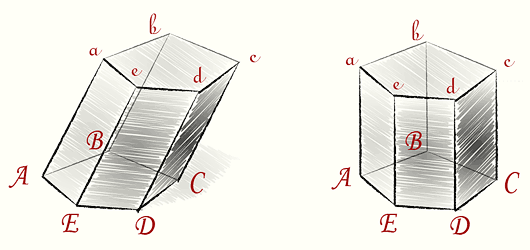Призма

Параллелограммы и т.д. называются боковыми гранями. Высотой призмы называется перпендикуляр опущенный из любой точки одного основания. на плоскость другого. Призма называется треугольной четырехугольной и т.д., смотря по тому, лежит ли в основании треугольник, четырехугольник и т.д.

Если боковые ребра призмы перпендикулярны к плоскости основания, то — призма прямая. Если нет — призма наклонная. Если в прямой призме основание — правильный многоугольник — призма правильная.

Перпендикулярное сечение призмы — это такое сечение, которое образовано плоскостью перпендикулярной к её боковому ребру.

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. Пирамида называется треугольной, четырехугольной, и т.д., если основанием пирамиды является треугольник, четырехугольник и т.д. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и т.д.

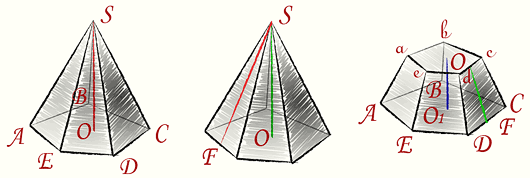Пирамида, Усеченная Пирамида