2014-02-09
2008
Теорема Чебышева. Если дисперсии независимых случайных величин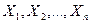 
ограничены одной и той же постоянной 
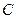, а число их достаточно велико, то, как бы мало ни было данное число 
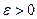, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превзойдёт 
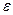по абсолютной величине, сколь угодно близка к единице.
.
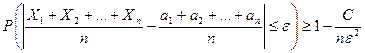Следствие. Если независимые случайные величины имеют одинаковые математические ожидания, равные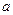 
: 
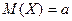, а их дисперсии ограничены одной и той же постоянной 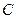, то теорема Чебышева имеет вид:
.
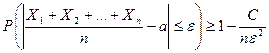Следствие является наиболее простой формой закона больших чисел.
Пример 7.2. Сколько надо провести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более, чем на 1 по абсолютной величине, если среднеквадратическое отклонение не превосходит 5?
Решение. Обозначим через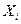
- результат 
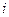-го измерения. Необходимо найти 
, при котором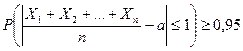 
.
Данное неравенство будет выполняться, если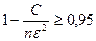 
.
Т.к.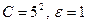 
неравенство имеет вид 
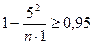. Решая его, получим
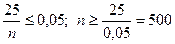. Т.е. потребуется не менее 500 измерений.
