Числовые характеристики зависимости - ковариация и корреляция

Ковариацией (совместной вариацией) cov(X, Y) СВ X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:

или .

Ковариация СВ X и Y есть математическое ожидание произведения центрированных величин.

Обобщение формулы для вычисления ковариации для ДСВ и НСВ:

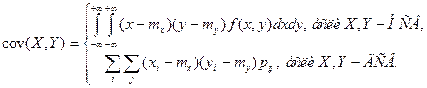
Для независимых СВ X и Y: cov (X,Y)=0 – необходимое, но не достаточное условие: если cov(X,Y)=0 – нельзя утверждать, что X и Y – независимые случайные величины.

Коэффициентом корреляции r_ху СВ X и Y есть отношение ковариации величин X и Y к произведению их средних квадратических отклонений

.

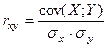Для существования коэффициента корреляции необходимо и достаточно существование дисперсий.

Свойства коэффициента корреляции:

1) 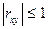, т.е. корреляция случайных величин принимает значение .

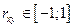2) 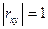тогда и только тогда, когда случайные величины X и Y линейно зависят друг от друга, т.е. .

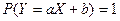Если случайные величины X и Y связаны линейной зависимостью 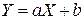, где a,b Î R, то коэффициент корреляции

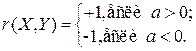
3) Коэффициент корреляции (попарно) независимых случайных величин X и Y равен нулю:

.

4) Т.о., коэффициент корреляции служит для оценки тесноты линейной связи между Х и Y: чем ближе к единице, тем связь сильнее, чем ближе к нулю, тем связь слабее.

Две СВ, имеющие r(X,Y)=0, называют некоррелированными, причем из независимости случайных величин следует их некоррелированность.

Если коэффициент корреляции r(X,Y)>0, то корреляция СВ X и Y положительная, если r(X,Y)<0 то корреляция отрицательная.

Положительная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем возрастать.

Отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.