Закон больших чисел. Последовательность случайных величин Х1, Х2, , Хn, сходится по вероятности к случайной величине X

Последовательность случайных величин Х ₁, Х ₂, …, Х_n,… сходится по вероятности к случайной величине X, если для любого e >0

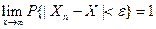или .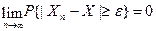

Символически сходимость по вероятности: X_n 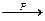X или X_n 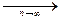X.

1) Неравенство Маркова (для оценки вероятности неотрицательных СВ).

Если X³0, "e >0 и неизвестен закон распределения: то

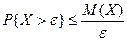, или .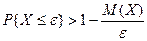

2) Неравенство Чебышева. Если СВ X имеет MX, DX – конечные и "e >0:

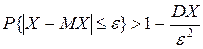и .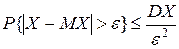

3) Теорема Чебышева. Если Х₁, Х₂, …, Х_n – последовательность попарно независимых СВ, MX, C – const, D(X₁)≤C, D(X₂)≤C, …, D(X_n)≤C,…,

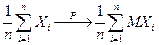, или "e >0,

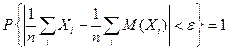или

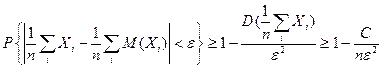при n ®¥ мало отличается от среднего арифметического их математических ожиданий M (X ₁), M (X ₂), …, M (X_n), т.е. обладает свойством статистической устойчивости.

Для одинаково распределенных случайных величин с конечной дисперсией D и M (x_i) =m: .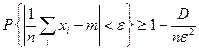

4) Теорема Бернулли ( частный случай теоремы Чебышева для независимых повторных испытаний).

Пусть вероятность успеха P(A)=p, m - число успешных испытаний из n, " e > 0:

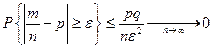, или

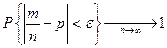или 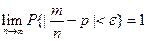т.е. относительная частота 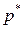числа успехов m в n испытаниях Бернулли обладает свойством статистической устойчивости.

Оценим .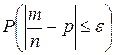

Т.к. 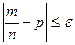, то 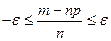. Если 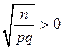, то:

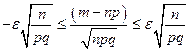Т.к. Ф (- x) = - Ф (x), то

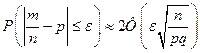Задача. «Опыт Бюффона» (X VIII век).

Найти вероятность того, что при повторении опыта Бюффона, относительная частота появления герба отклонится от вероятности по модулю не более чем в опыте Бюффона.

Решение: 1)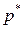=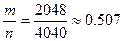, где 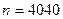, , 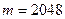а теоретическая вероятность p= 1 / 2. Оценим

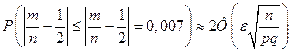или

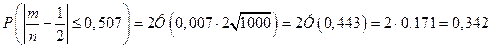Опыты	Число испытаний	Относительная частота	Отклонение относительной частоты от вероятности
Опыт Бюффона		0,5069	0,0069
Первый опыт Пирсона		0,5016	0,0016
Второй опыт Пирсона		0,5005	0,0005