Начальным моментом порядка k случайной величины X называют математическое ожидание для случайной величины 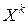 :
:
nk=M (Xk), где k Î R.
При k =1 имеем первый начальный момент n 1 =MX=m, который, как известно, есть математическое ожидание случайной величины X.
Отклонение для случайной величины X от своего математического ожидания X – MX называется центрированной случайной величиной X.
Центрирование случайной величины – перенос начала координат в среднюю точку – центр распределения.
Центральным моментом порядка k для случайной величины X есть математическое ожидание степени k соответствующей центрированной случайной величины X:
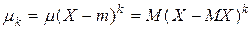 , где k Î R
, где k Î R
Зависимость между начальным и центральным моментом порядка s выражается формулами:
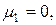
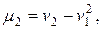
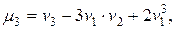
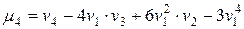 и т.д.
и т.д.
Первые четыре центральных момента:
1) 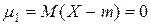 – есть математическое ожидание центрированной случайной величины X или первыйцентральный момент;
– есть математическое ожидание центрированной случайной величины X или первыйцентральный момент;
2) 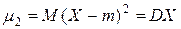 – дисперсия случайной величины X или второй центральный момент;
– дисперсия случайной величины X или второй центральный момент;
3) 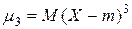 – третий центральный момент;
– третий центральный момент;
4) 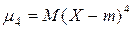 – четвертый центральный момент.
– четвертый центральный момент.
Зависимость моментов от характера распределения СВ
| Виды моментов | Виды распределений | |
| ДСВ | НСВ | |
| Начальный момент порядка k | 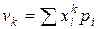
| 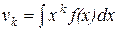
|
| Центральный момент порядка k | 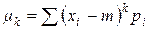
| 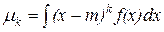
|
Первый начальный момент 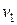 – «центр распределения».
– «центр распределения».
M(X) – первый начальный момент – это средняя точка распределения.
D(X) – второй центральный момент –разброс вокру г M(X).
Асимметрия распределения: 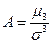 .
.
Если, распределение симметрично относительно своего центра, то A =0.
Эксцесс –«плосковершинность» распределения: 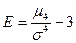 .
.
Для нормального распределения 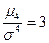 ® E =0. Для распределений, близких к нормальному, E ≠0 показывает степень различия между имеющимся распределением и нормальным. Если
® E =0. Для распределений, близких к нормальному, E ≠0 показывает степень различия между имеющимся распределением и нормальным. Если 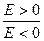 ,токривая распределений имеет более
,токривая распределений имеет более 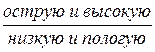 вершину.
вершину.
Значения асимметрии и эксцесса для различных распределений:
| Вид распределения | Асимметрия | Эксцесс |
| Нормальное X ~N(m, s) | A =0 | E =0 |
| Равномерное X ~U(a, b) | A =0 | E = -1.2 |
| Показательное X ~E(l) | A =2 | E =6 |
| Биномиальное X ~Bi(n, p) | 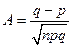
| 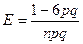
|
| Геометрическое X ~G(p) | A =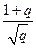
| E=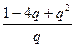
|
| Пуассона X ~П(l) | 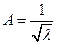
| 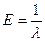
|
 2014-02-09
2014-02-09 427
427







