В основе лежит гипотеза плоских сечений – сечения после деформации остаются плоскими и перпендикулярными оси бруса. В тех деформациях, где эта гипотеза экспериментально подтверждается, можно получить теоретически выражения для распределения напряжений по сечению и для распределения деформаций по оси бруса.
Растяжение-сжатие (презентация).
Закон распределения напряжений в поперечном сечении равномерный, т.е. во всех точках сечения напряжения одинаковы: s = N /A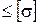 - условие прочности при растяжении – сжатии. Перемещение сечения с координатой х относительно начального сечения:
- условие прочности при растяжении – сжатии. Перемещение сечения с координатой х относительно начального сечения:
 .
.
Удлинение (укорочение) участка длиной 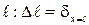
По закону Гука 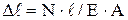 .
.
Сдвиг.
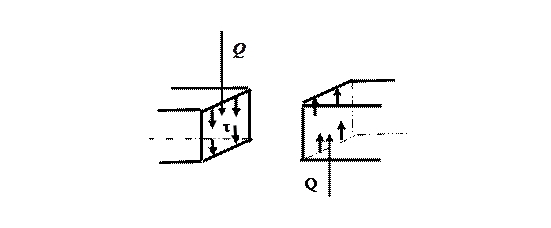
Закон распределения напряжений условно принят равномерным: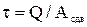
Условие прочности при сдвиге: 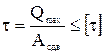 .
.
Определение поверхности сдвига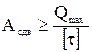 .
.
Определение максимальной силы сдвига: 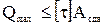 .
.
Кручение.
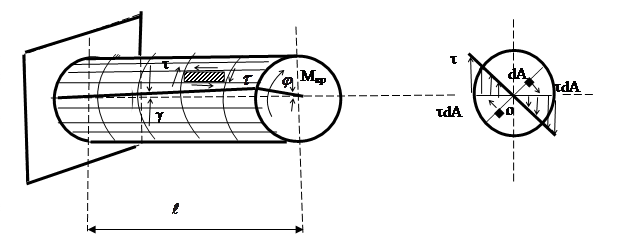
Гипотеза плоских сечений подтверждается только для бруса круглого сечения. Касательное напряжение в любой точке сечения
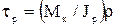 ,
,
Максимальный напряжения возникают на контуре сечения где r – радиус точки, в которой определяются напряжения, Jr – полярный момент инерции сечения (для круглого сечения
Jr=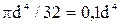
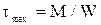 ,
,
где Wp=Jp/(d/2) - полярный момент сопротивления 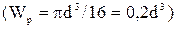 .
.
Условия прочности при кручении: 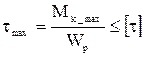 .
.
Диаметр вала из условия прочности: 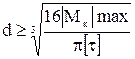 .
.
Максимальный момент: Мк_max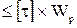 .
.
Угол закручивания сечения с координатой х относительно начального сечения:
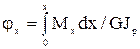 , при х = l
, при х = l 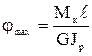
Плоский изгиб.
|
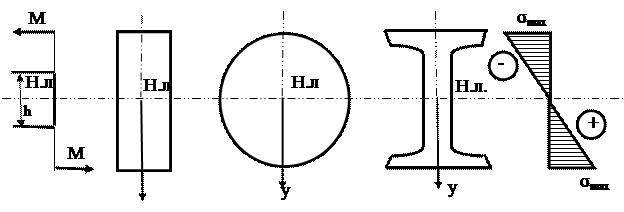
Закон распределения нормальных напряжений в сечении балки вдоль оси У
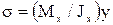 ,
,
где у – координата точки, в которой определяется напряжение, Jx – осевой момент инерции сечения.
Максимальные напряжения возникают в наиболее удаленных точках сечения: 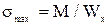 ,
,
где Wx=Jx/(h/2) – осевой момент сопротивления сечения.
Для прямоугольного сечения Jx= bh3 /12; Wx= bh2 /6; для круглого сечения Jx=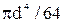 ; Wx=
; Wx=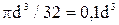 Для двутавров, швеллеров, уголков – значения J,W приведены в таблицах.
Для двутавров, швеллеров, уголков – значения J,W приведены в таблицах.
Условие прочности при изгибе: 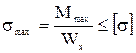 .
.
 2014-02-09
2014-02-09 468
468








