2014-02-09
756
О. 1. Если проводится несколько испытаний, причем вероятность появления события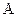 
в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события .
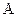Пусть проводится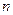 
независимых испытаний, в каждом из которых возможно только два исхода: либо событие 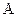появится, либо нет.
Условимся считать, что вероятность события 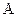в каждом испытании одна и та же и равна 
.
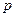Тогда вероятность ненаступления события 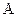в каждом испытании так же постоянна и равна 
.
Выше описанная совокупность условий называется схемой независимых испытаний Бернулли.
Теорема 1. Если вероятность 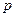наступления события 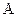в каждом из независимых испытаний постоянна, то вероятность 
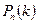того, что в 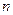независимых испытаниях событие 
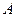появится ровно 
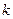раз, вычисляется по формуле
.
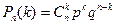Пример 1. В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятность появления мальчика в семье равной 0.515, определить вероятность появления в ней двух мальчиков.
Решение: 
.
