Теорема. Если событие 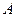 может наступить только при условии появления одного из несовместных событий
может наступить только при условии появления одного из несовместных событий 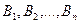 , которые образуют полную группу, то вероятность события
, которые образуют полную группу, то вероятность события 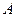 равна сумме произведений каждого из этих событий на соответствующие условные вероятности события
равна сумме произведений каждого из этих событий на соответствующие условные вероятности события 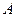 , т. е.
, т. е.
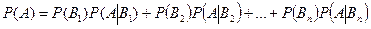 .
.
Поскольку заранее не известно, какие из событий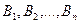 наступят, то их называют гипотезами.
наступят, то их называют гипотезами.
Часто, приступая к анализу вероятностей, мы имеем предварительные значения вероятностей, интересующих нас событий. После проведения испытания эти вероятности могут несколько уточняться.
Пусть произведено испытание, в результате которого появилось событие 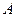 . Необходимо найти вероятности гипотез
. Необходимо найти вероятности гипотез 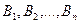 , после того как испытание произведено, т. е. условные вероятности гипотез
, после того как испытание произведено, т. е. условные вероятности гипотез 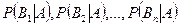 .
.
Найдем сначала условную вероятность 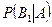 .
.
По теореме умножения 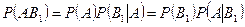 .
.
Отсюда 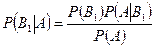 .
.
Аналогично выводятся формулы остальных гипотез.
В общем случае условная вероятность любой гипотезы 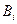 , где
, где 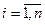 , определяется как
, определяется как 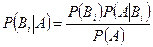 .
.
Последняя формула называется формулой Байеса. Она позволяет переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие 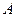 .
.
Пример 1. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 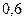 , а ко второму -
, а ко второму - 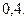 Вероятность того, что деталь будет признана стандартной первым контролером, равна
Вероятность того, что деталь будет признана стандартной первым контролером, равна 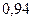 , а вторым -
, а вторым - 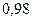 .
.
Найти вероятность того, что деталь будет признана стандартной;
Проверенная деталь признана стандартной. Найти вероятность того, что она проверена первым контролером.
Решение: Событие 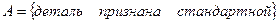 ,
,
Гипотеза 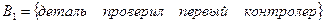 ,
,
Гипотеза 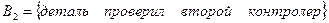 .
.
1) 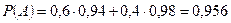 ;
;
2) 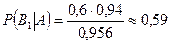
Т.о. до испытания значение вероятности гипотезы 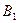 равнялось
равнялось 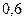 , а после проведения испытания изменилось и стало равняться
, а после проведения испытания изменилось и стало равняться 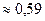 .
.
 2014-02-09
2014-02-09 1162
1162
