Если число испытаний 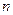 достаточно велико, а вероятность появления события
достаточно велико, а вероятность появления события 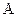 в каждом испытании постоянна и равна
в каждом испытании постоянна и равна 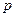 , причем
, причем 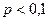 , то применение формулы Муавра-Лапласа становится невозможным.
, то применение формулы Муавра-Лапласа становится невозможным.
Теорема 1. Если вероятность 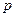 появления события
появления события 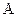 в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний, причем произведение
в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний, причем произведение 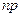 сохраняет постоянное значение, т. е.
сохраняет постоянное значение, т. е. 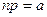 , то вероятность
, то вероятность 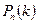 того, что в
того, что в 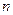 независимых испытаниях событие
независимых испытаниях событие 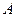 появится
появится 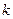 раз удовлетворяет предельному равенству:
раз удовлетворяет предельному равенству:
 (2).
(2).
Строго говоря, условие теоремы 2: 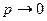 при
при 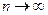 , нарушает исходные предпосылки в схеме независимых испытаний Бернулли, в которой
, нарушает исходные предпосылки в схеме независимых испытаний Бернулли, в которой 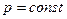 . Однако, если вероятность
. Однако, если вероятность 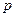 постоянна и достаточно мала, а число
постоянна и достаточно мала, а число 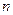 испытаний велико, причем произведение
испытаний велико, причем произведение  незначительно, то из предельного равенства (2) можно записать приближенную формулу Пуассона:
незначительно, то из предельного равенства (2) можно записать приближенную формулу Пуассона: 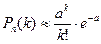 .
.
Пример 3. Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0.002. Найти вероятность того, что при транспортировке будет повреждено три изделия.
Решение: В данном случае формула Бернулли не применима, т. к. придется возводить 0. 002 в 500-ю степень.
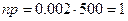 ;
;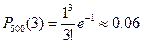 .
.
 2014-02-09
2014-02-09 2638
2638
