Закон больших чисел

Поскольку на практике сведения о каждой случайной величине, чаще всего, являются очень скромными и уверенно предсказать какое возможное значение она примет затруднительно, то может показаться, что нельзя установить закономерности поведения и суммы достаточно большого числа случайных величин. Оказывается, что это не так.

Закон больших чисел в широком смысле – это общий принцип, согласно которому совокупное действие большого числа случайных величин приводит, при некоторых сравнительно широких условиях, к результату, почти независящему от случая, т.е. при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью точности.

Терема 1. (неравенство Маркова)

Если случайная величина 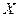принимает только неотрицательные значения, то для любого числа 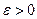выполняется неравенство: .

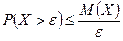Для события 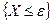, противоположного событию 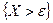, неравенство Маркова может быть записано в виде: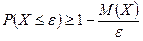

Теорема 2. (неравенство Чебышева)

Вероятность того, что отклонение случайной величины 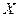от ее математического ожидания по абсолютной величине меньше любого числа 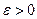, не меньше чем 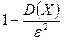, т.е. .

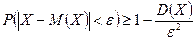Для события 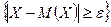, противоположного событию 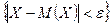, неравенство Чебышева может быть записано в виде: .

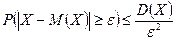Теорема 3. (теорема Чебышева) Если 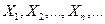- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа 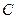), то, как бы мало ни было 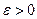, вероятность неравенства:

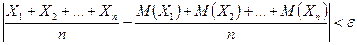
будет как угодно близка к единице, если число случайных величин достаточно велико.

Замечание 1. Теорема Чебышева утверждает, что если рассматривается достаточно большое число случайных величин, имеющих равномерно ограниченные дисперсии и являющиеся независимыми, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Теорема 4. (частный случай теоремы Чебышева)

Если 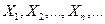- попарно независимые случайные величины, имеющие одинаковые математические ожидание 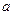, и их дисперсии равномерно ограничены (не превышают постоянного числа 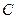), то, как бы мало ни было 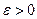, вероятность неравенства:

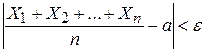
будет как угодно близка к единице, если число случайных величин достаточно велико.

Сущность теоремы Чебышева: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу 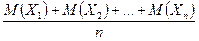. Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Значение теоремы Чебышева для практики:

При измерении некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. Теорема Чебышева указывает условия, при которых указанный способ может быть применен.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов.

Пусть выполнены условия схемы независимых испытаний Бернулли, причем 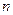достаточно велико.

Теорема 5. (теорема Бернулли) Если в каждом из 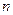независимых испытаний вероятность 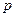события 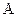постоянна, то вероятность того, что отклонение относительной частоты от вероятности 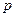по абсолютной величине будет сколь угодно малым, будет как угодно близка к единице если число испытаний достаточно велико, т.е.

.

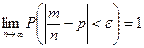Сущность теоремы Бернулли: теорема Бернулли позволяет предвидеть, какова примерно будет относительная частота появления события.