Пусть непрерывная случайная величина 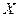 задана плотностью распределения
задана плотностью распределения 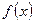 . Тогда аналогично ДСВ для НСВ могут быть определены числовые характеристики.
. Тогда аналогично ДСВ для НСВ могут быть определены числовые характеристики.
О.1. Математическим ожиданием 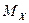 НСВ
НСВ 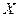 , возможные значения которой принадлежат всей оси
, возможные значения которой принадлежат всей оси 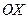 , называют определенный интеграл:
, называют определенный интеграл:
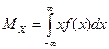 .
.
O.2. Дисперсией 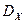 НСВ
НСВ 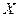 , возможные значения которой принадлежат всей оси
, возможные значения которой принадлежат всей оси 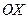 , называется значение интеграла
, называется значение интеграла
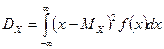 .
.
Замечание 1. Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ.
Замечание 2. На практике для вычисления дисперсии удобно пользоваться формулой: 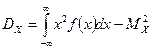 .
.
O.3. Средним квадратическим отклонением 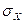 НСВ
НСВ 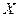 называется корень квадратный из дисперсии, т.е.
называется корень квадратный из дисперсии, т.е.
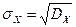 .
.
О.4. Модой 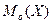 НСВ
НСВ 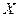 называется такое значение этой величины, плотность вероятности которого максимальна.
называется такое значение этой величины, плотность вероятности которого максимальна.
O.5. Медианой 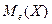 НСВ
НСВ 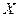 называется такое значение этой величины, что выполняется равенство:
называется такое значение этой величины, что выполняется равенство:
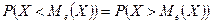 .
.
Пример 1. НСВ 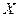 задана плотностью распределения вероятностей
задана плотностью распределения вероятностей 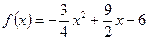 в интервале
в интервале 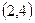 . Вне этого интервала
. Вне этого интервала 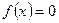 . Найти все числовые характеристики НСВ
. Найти все числовые характеристики НСВ 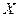 .
.
Решение:
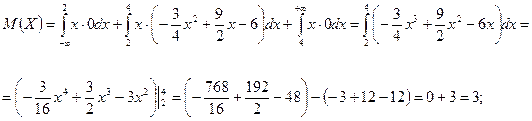
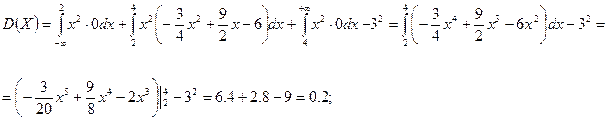
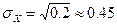
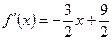 ;
;
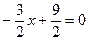 ;
;
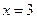 ;
;
 ;
;
Т. к. кривая распределения – парабола симметричная относительно
прямой 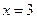 , то
, то 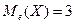 .
.
 2014-02-09
2014-02-09 6312
6312








