О.1. Плотностью распределения вероятностей (дифференциальной функцией) непрерывной случайной величины 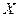 называется функция
называется функция 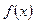 , равная первой производной от функции распределения
, равная первой производной от функции распределения 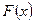 , т.е.
, т.е.
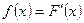 .
.
Свойства функции 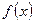 :
:
- Плотность распределения неотрицательная функция, т.е.
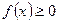 .
. - Несобственный интеграл от плотности распределения на интервале
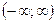 равен единице, т.е.
равен единице, т.е.
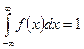 .
.
- Если все возможные значения случайной величины принадлежат интервалу
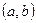 , то
, то
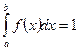 .
.
4. Вероятность попадания случайной величины в интервал 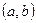 может быть вычислен по формуле (Ньютона-Лейбница):
может быть вычислен по формуле (Ньютона-Лейбница):
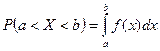 .
.
5. Если известна плотность распределения 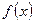 , то функция распределения
, то функция распределения 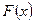 может быть найдена по формуле:
может быть найдена по формуле:
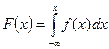
Пример 3. НСВ 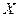 задана плотностью распределения
задана плотностью распределения
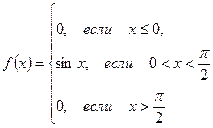 .
.
Найти функцию распределения вероятностей и построить графики 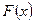 и
и 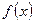 . Найти вероятность того, что в результате испытания случайная величина
. Найти вероятность того, что в результате испытания случайная величина 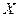 примет значение из интервала
примет значение из интервала 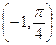 .
.
Решение:
при 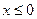 :
: 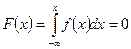 ;
;
при 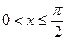 :
: 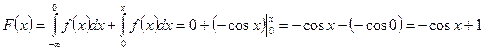 ;
;
при 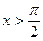 :
: 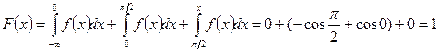 ;
;
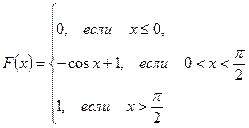 .
.
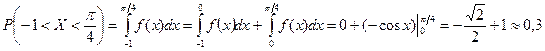 .
.
 2014-02-09
2014-02-09 789
789








