Предварительные понятия газовой динамики

Совместное применение нескольких фундаментальных законов

Лекция №3.

Законы сохранения массы, импульса, энергии используем для построения математической модели, описывающей течение сжимаемого газа. Обсудим отличия полученной модели от моделей, полученных ранее, а также некоторые следующие из нее свойства газодинамических движений.

Заметное изменение плотностей жидкостей и твердых тел может достигаться лишь при огромных давлениях в десятки и сотни тысяч атмосфер и выше. Газообразные среды гораздо легче подвергаются сжатию: при перепаде давления в одну атмосферу плотность газа, первоначально находившегося при атмосферном давлении, уменьшается или увеличивается на величину, сопоставимую с начальной его плотностью.

В газовой динамике, изучающей движение сжимаемых сред под действием каких-либо внешних сил или сил давления самого вещества, считается выполненным неравенство 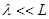, где 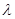- длина свободного пробега, 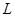- характерные размеры области рассматриваемого течения (сплошная среда).

Считается также выполненной гипотеза о ЛТР. В условиях ЛТР сжимаемую среду можно рассматривать как совокупность большого числа жидких частиц, с размерами, много большими 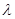, но много меньшими, чем 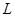. Для каждой такой частицы, связанной с небольшой фиксированной массой среды, вводятся характеризующие ее средние величины – плотность 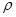, давление 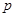, температура 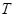, внутренняя энергия 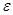и т.д., а также скорость 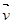ее макроскопического движения как единого целого.

Все эти величины в общем случае зависят от трех пространственных переменных 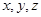и времени 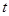. В дальнейшем будем также предполагать отсутствие в среде процессов теплопередачи, вязкого трения, источников и стоков энергии, например, излучения, и, кроме того, отсутствие внешних объемных сил и источников (стоков) массы в веществе.