2014-02-09
1204
Для их получения применим второй закон Ньютона к элементарной жидкой частице, имеющей в некоторый момент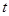 
форму куба с гранями 
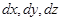(рис. 3.1).
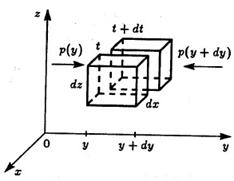
Рис. 3.1
Жидкая частица – это перемещающаяся в пространстве и меняющий свою форму объем, содержащий в разные моменты времени 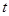одни и те же атомы и молекулы газа. Тем самым его масса 
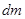постоянная. Для простоты вывода будем считать, что за короткое время 
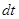куб не меняет своей формы и смещается по всем направлениям на расстояние, много меньшее его размеров.
Определим сначала силу, действующую на куб, например в направлении оси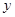 
. Она, очевидно, равна разности давлений на левой и правой границах, умноженной на их площади (иных сил по предположению нет):
.
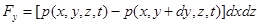Сила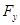 
равна ускорению жидкой частицы в направлении 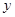, умноженному на его массу 
:
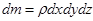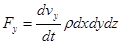. (5)
Заменяя в правом выражении для 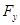разность давлений через производную от давления по 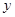и приравнивая его к (5), приходим к уравнению, описывающему движение газа вдоль оси :
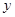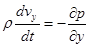. (6)
Точно также получаем уравнения движения по направлениям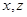 
:
|
|
|
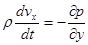, (7)
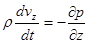, (8)
имеющие как и в (6), очевидный физический смысл. В векторной форме уравнения (6) – (8) имеют вид
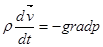. (9)
Поясним, что (6) – (9) через 
обозначена полная (субстанциональная, т.е связанная частицами газа) производная по времени какой-либо величины, характеризующей данную неизменную массу газа.
Раскрыв через частные производные по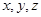 
и 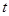в соответствии с правилом 
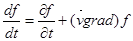, придем к уравнениям движения Эйлера
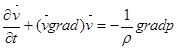. (10)
Будучи записаны покоординатно, они принимают вид
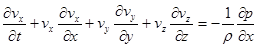, (11)
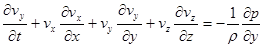, (12)
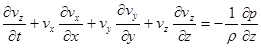. (13)
В отличие от течения грунтовых вод, градиенты давления в уравнениях газа (6) – (13) определяют компоненты ускорения вещества, а не компоненты его скорости (сравнение с законом Дарси). Уравнения (4), (11) – (13) содержат пять неизвестных величин -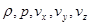 
. Для их замыкания естественно использовать закон сохранения энергии.
