2014-02-09
1934
Применим рассуждения, аналогичные тем, которые использовались для вывода уравнений неразрывности для течения грунтовых вод и процесса теплопередачи. Рассмотрим в некоторой области пространства, занятой движущимся газом, элементарным кубом со сторонами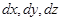 
и подсчитаем в нем баланс массы за время 
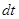(рис. 2.1).
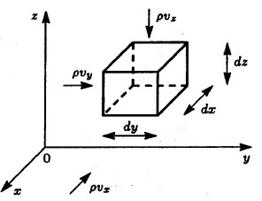
Рис. 2.1
Здесь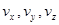 
– компоненты скорости по соответствующим осям. По оси 
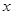через грань с координатой 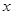в кубик за время 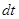поступает масса газа, равная
,
поскольку величина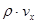 
ничто иное, как поток массы по направлению оси 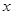. За то же самое время из грани с координатой 
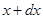вытекает масса
,
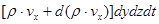где через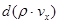 
обозначено приращение потока массы при переходе от координаты 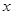к координате 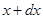. Суммируя оба последних выражения и учитывая, что
,
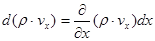получаем величину изменения массы в кубе за время 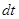благодаря движению газа вдоль оси :
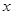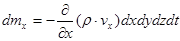. (1)
Таким же образом находим изменения массы за счет движения по осям 
:
,
. (2)
В фиксированном объеме куба изменение находящейся в нем массы газа выражается также через изменение его плотности со временем:
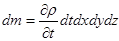. (3)
Суммируя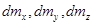 
и приравнивая результат к 
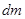, получаем из (1) – (3) искомое уравнение неразрывности
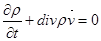, (4)
выражающее закон сохранения массы вещества применительно к движению сжимающегося газа. По своей форме и смыслу (скорость изменения величины определяется дивергенцией потока этой величины) оно вполне аналогично уравнению неразрывностью. Однако аналогия с течением грунтовых вод на этом заканчивается. При свободном движении газа его динамика определяется лишь силами давления самого газа, в отличие от движения жидкости, испытывающей сопротивление сил грунта.
