Опр.: 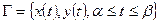
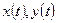 - гладкие функции
- гладкие функции
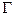 - параметризованная кривая
- параметризованная кривая
Если 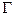 - замкнутая кривая (контур), то:
- замкнутая кривая (контур), то:
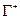 - прохождение контура против часовой стрелки (положительная ориентация)
- прохождение контура против часовой стрелки (положительная ориентация)
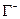 - прохождение контура по часовой стрелке (отрицательная ориентация)
- прохождение контура по часовой стрелке (отрицательная ориентация)
Опр.: 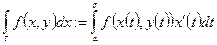 .
.
Опр.:
Область 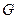 называется элементарной, если:
называется элементарной, если: 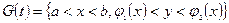
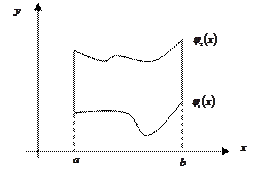
Лемма: Формула Грина.
Если: 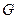 - элементарная область
- элементарная область
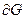 - кусочно гладкая,
- кусочно гладкая, 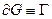 ,
,
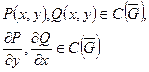
То: 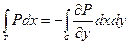
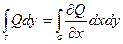
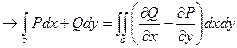
Док-во:
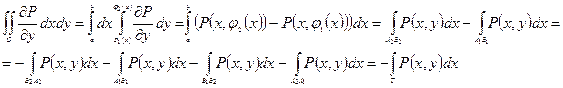
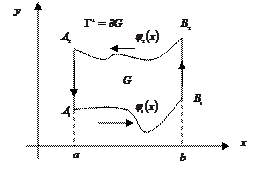
Замечание:
В силу аддитивности формула Грина справедлива и для областей, которые можно разбить на конечное число элементарных.
Замена переменных (двумерный случай).
Утв.:
Если: 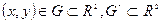
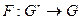 - диффеоморфизм,
- диффеоморфизм,
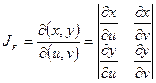 ,
,
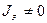
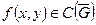 ,
,
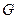 - элементарная область
- элементарная область
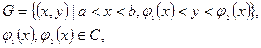
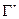 - положительно ориентированная граница
- положительно ориентированная граница 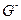 ,
,
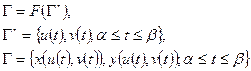
То: 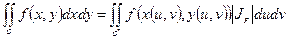
Док-во:
По нашим предположениям оба интеграла существуют как интегралы от непрерывных функций по измеримым множествам.
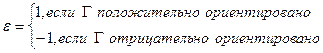
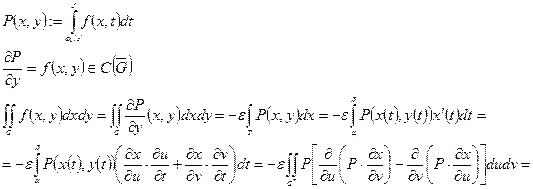
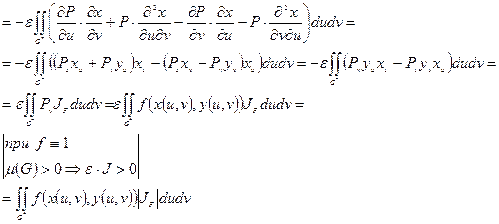
Следствие:
Если якобиан положительный (отрицательный), то отображение сохраняет (меняет) ориентацию контура.
 2014-02-09
2014-02-09 911
911








