Общие свойства интеграла

1. Линейность

а) 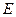- допустимое множество 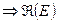является линейным пространством (в силу критерия Лебега и того, что объединение множеств меры ноль есть множество меры ноль)

б) 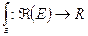интеграл – линейный функционал на .

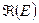Замечание:

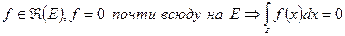
2. Аддитивность

а) Если 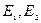- допустимые множества и 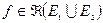, тогда 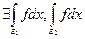т.е.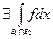

б) если кроме тог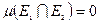о , то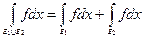

Док-во:

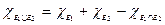
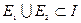
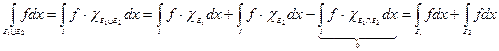
3.Оценка интеграла

а) 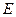- допустимое, .

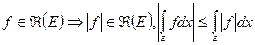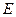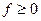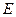Утв.: - допустимое множество, на почти всюду .

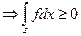Следствие 1.

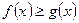почти для всех .

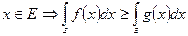Следствие 2.

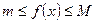почти для всех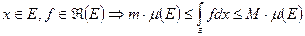

Следствие 3.

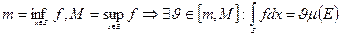
Следствие 4.

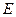- связное множество,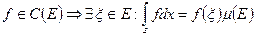

Следствие 5.

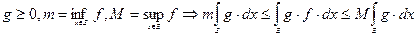
Лемма:

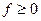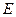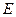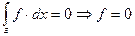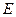на почти всюду, - допустимое, на почти всюду.

Док-во:

рассмотрим промежуток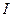

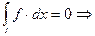
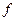непрерывна почти всюду на 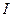, покажем что 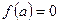, где 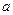- точки непрерывности функции .

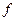Предположим противное:

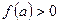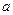, -точки непрерывности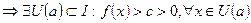

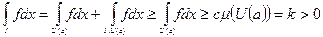- противоречие. Далее переходим к 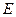через характеристическую функцию.