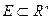2014-02-09
1678
называется допустимым, если оно ограничено и его граница 
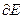имеет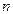 
-мерную лебегову меру ноль (
).
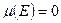Пр.: Куб, сфера и пр.
Лемма.
:
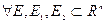1. 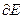замкнуто в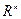 
2. 
3. 
4. 
Замечание:
Для бесконечного числа множеств это не верно.
Следствия:
- Граница допустимого множества – компакт.
- Объединение, пересечение и разность конечного числа допустимых множеств - допустимое множество.
из его покрытия системой открытых множеств можно выделить конечное покрытие, такое что: 
Опр.: Говорят, что множество имеет жорданову меру ноль (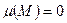
), если:
Замечание:
Для границы множества жорданова мера ноль эквивалентна лебеговой.
Опр.: Характеристической функцией множества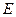 
называется функция:
Замечание:
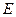-допустимо 
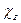почти всюду непрерывна (т.к. 
)
Интеграл по множеству.
Опр.:
Опр.:
Мерой Жордана допустимого множества называется интеграл по этому множеству от единичной функции: 
Утв.: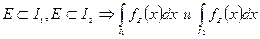 
существуют или не существуют одновременно, а если существуют, то равны.
Док-во:
Функция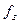 
отлична от нуля только внутри 
(
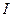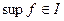- носитель функции 
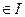) множество точек разрыва 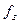принадлежит 
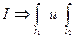отличаются нулевыми слагаемыми.
Th.: Критерий Лебега интегрируемости функции по множеству.
Геометрический смысл меры Жордана
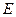- допустимое множество,
Нижняя интегральная сумма Дарбу есть сумма объёмов промежутков, целиком принадлежащих множеству .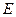
Верхняя интегральная сумма Дарбу есть сумма объёмов промежутков, имеющих с множеством 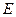общие точки.
Опр.:
- Если существует предел нижних сумм Дарбу, то он называется внутренней мерой Жордана.
- Если существует предел верхних сумм Дарбу, то он называется внешней мерой Жордана.
- Если внешняя и внутренняя меры Жордана совпадают, то множество называется измеримым по Жордану.
Утв.:
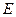- измеримо по Жордану 
