Контрольные вопросы к лекции 9
1. На каких принципах возможно классифицировать СМО?
2. Скажите, что означает запись M/M/5?
3. Что мы получим, решив систему дифференциальных уравнений Колмогорова для вероятностей состояний?
4. При каких условиях существуют финальные вероятности?
5. В каком случае дифференциальные уравнения Колмогорова преобразуются в систему алгебраических уравнений? Объясните физический смысл этого превращения.
6. Какие величины связывает формула Литтла и для каких законов распределения она справедлива?
Многоканальная СМО с отказами (задача Эрланга)
Начнем рассмотрение с одной из простейших задач, которая возникла в начале 20 века при изучении работы телефонных станций. Изучалась эффективность работы телефонной станции, имеющей n каналов обслуживания (барышень, сидящих на коммутаторе). Все входящие потоки вызовов полагались простейшими. Интенсивность входного потока полагалась равной -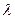 Интенсивность обслуживания -
Интенсивность обслуживания - 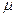 .
.
Таким образом, СМО с отказами является такая система, в которой приходящие для обслуживания требования, в случае занятости всех каналов обслуживания, сразу ее покидают.
|
|
|
Найти:
 - финальные вероятности
- финальные вероятности
A- абсолютную пропускную способность
Q- относительную пропускную способность
 - вероятность отказа
- вероятность отказа
 - среднее число занятых каналов
- среднее число занятых каналов
если все n каналов заняты, то заявка получает отказ.
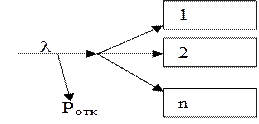
1. Введём множество состояний:
S0- все каналы пусты
S1- один канал занят
S2- два канала заняты
Sn- n каналов заняты.
2. Составим граф состояний:
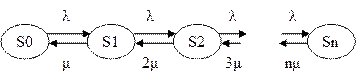
Обратите внимание на «разметку» нижних стрелок графа. Коэффициенты при интенсивности обслуживания возрастают с увеличением номера состояния. Это связано с тем, что если работают два канала, то обслужить свою заявку может каждый из них и суммарная интенсивность перехода в предыдущее состояние, где работает только один канал (любой из этих двух), равна  , если работают три канала, то, соответственно, -
, если работают три канала, то, соответственно, -  и т.д.
и т.д.
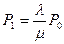
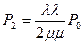
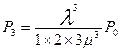
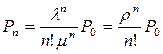
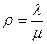
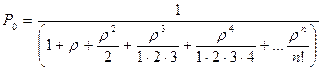
эти формулы называются формулами ЭРЛАНГА.
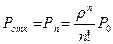
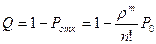
Q – относительная пропускная способность показывает вероятность того, что заявка будет обслужена.
 ,
,
где А - абсолютная пропускная способность есть поток на выходе системы в абсолютных величинах за единицу времени.
Пример. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Пусть среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 ч-1. Найти вероятность отказа и среднее число занятых ЭВМ.
Имеем: m=3, l=0,25 ч-1,  =3 ч. Находим:
=3 ч. Находим:
|
|
|
 ,
,
 ,
,
 ,
,
 .
.
Таким образом, 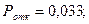
 ЭВМ.
ЭВМ.
Одноканальная СМО с неограниченной очередью (М/М/1)
Это одна из наиболее часто используемых моделей, относящихся к СМО с ожиданием. При ее рассмотрении принимаются следующие предположения:
- входной поток заявок (требований) - пуассоновский;
- время обслуживании распределено по экспоненциальному закону.
 - среднее время обслуживания.
- среднее время обслуживания. 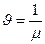
Найти:
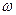 - среднее время ожидания
- среднее время ожидания
U- среднее время пребывания
 - средняя длина очереди
- средняя длина очереди
N- среднее количество заявок в системе
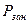 - вероятность занятости устройства.
- вероятность занятости устройства.
Будем определять характеристики этой СМО по уже рассмотренному в предыдущем случае алгоритму.
1. Введем множество состояний:
S0- канал (система) свободен
S1- одна заявка в СМО или канале и она обслуживается;
S2- две заявки в СМО - одна обслуживается, одна в очереди;
S3- три заявки в СМО – одна обслуживается, две в очереди;
Sn- n заявок в СМО – одна обслуживается, n-1 в очереди.
2.Составим граф состояний и разметим его.
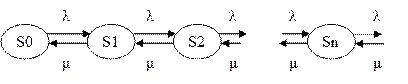
Для этой системы финальные вероятности существуют при  , если
, если  .
.
При 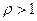 и
и  очередь возрастает неограниченно.
очередь возрастает неограниченно.
При  система справляется с потоком, если он регулярный.
система справляется с потоком, если он регулярный.
3. По формулам для процесса гибели и размножения имеем:
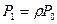 ;
;  ;
;  ;
;
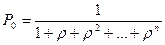
Вероятность того, что система пуста: 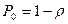
4. Определим характеристики эффективности
Среднее количество заявок в системе: 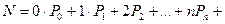 …
…
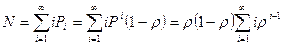
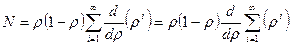
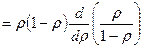
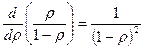
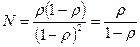
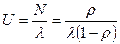
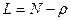
Вероятность занятости системы: 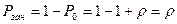
Среднее время ожидания заявок в очереди: 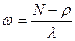
Многоканальная СМО с неограниченной очередью (М/М/n)
Для рассмотрения этой СМО снова применим уже использованный нами алгоритм рассмотрения:
1. Зададим множество состояний:
S0 – система пуста;
S1 – один канал занят;
S2 – два канала заняты;
Sn – n каналов заняты;
Sn+k – n каналов заняты, k заявок в очереди..
2. Составим граф состояний и разметим его.
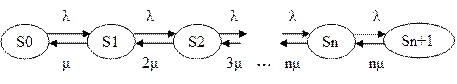
3. По формулам гибели и размножения найдем финальные вероятности.
Финальные вероятности существуют если 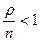
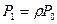
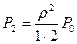 …
… 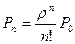
 …
… 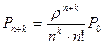
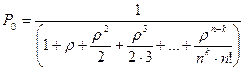
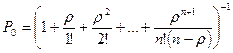
4. Характеристики эффективности.
Среднее число занятых каналов: 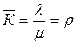

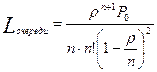
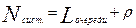
По формуле Литтла: 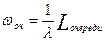
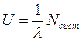
Пример. В порту имеется два причала для разгрузки грузовых судов. Интенсивность потока судов равна 0,8 судов в сутки. Среднее время разгрузки одного судна составляет 2 сут. Предполагается, что очередь ожидающих разгрузки судов может быть неограниченной длины.
Найти среднее время пребывания судна в порту.
Имеем: m=2, l=0,8 сут-1, 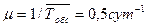 ,
,  .
.
Находим:
 ;
;
 ;
;
 .
.
Итак,  сут.
сут.
Частным случаем рассмотренной нами системы является СМО, в которой очередь не бесконечна, а имеет конечное значение. Этот случай рассматривается ниже
СМО с ограниченной длиной очереди.
СМО с ограниченной длиной очереди является такая система, в которой требование, поступающее на обслуживание, покидает систему, если заняты все каналы обслуживания, и в накопителе заняты все места.
Вероятности состояний S0, S1,…, SN находят по формуле
 , где
, где 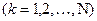 .
.
Вероятности состояний  определяют с помощью формулы
определяют с помощью формулы
 , где
, где  , l – максимальная длина очереди.
, l – максимальная длина очереди.
Вероятность P0 подсчитывают по формуле  .
.
В большинстве практических задач должно соблюдаться отношение 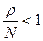 , тогда выражение для P0 можно переписать в следующем виде
, тогда выражение для P0 можно переписать в следующем виде
 .
.
Вероятность отказа в обслуживании определяется из выражения
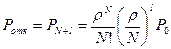 .
.
Среднее число каналов, занятых в обслуживании, и коэффициент занятости определяются:
 ;
;  .
.
Среднее число свободных аппаратов и коэффициент простоя определяются:
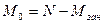 ;
;  .
.
Средняя длина очереди определяется с помощью выражения:
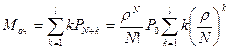 .
.
Пример. На автозаправочной станции установлены три колонки для выдачи бензина. Около станции находится площадка на три машины для их ожидания в очереди. На станцию прибывает в среднем две машины в минуту. Среднее время заправки одной машины 1мин. Требуется определить вероятность отказа и среднюю длину очереди.
Имеем: N=3, l=3, l=2мин-1,  =1мин,
=1мин,  . Находим:
. Находим:  ,
, 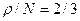 , тогда
, тогда
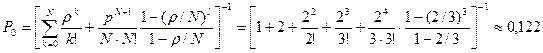 ,
,
 ,
,
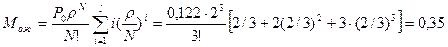 .
.
Таким образом,  ,
,  машины.
машины.
 2014-02-09
2014-02-09 3140
3140








