В динамике рассматривается влияние взаимодействия между телами на их механическое движение.
Основная задача динамики состоит в определении положения тела в произвольный момент времени по известному начальному положению, начальной скорости и силам, действующим на тело.
При решении обратной задачи нужно уметь по закону движения тела определять действующие на него неизвестные силы.
Опыт показывает, что изменение состояния покоя или равномерного и прямолинейного движения любого тела происходит только при взаимодействии тел.
Если же взаимодействие отсутствует или скомпенсировано, то тело будет сохранять состояние покоя или равномерного и прямолинейного движения. Первым к этому выводу пришел Галилео Галилей.
Но движение относительно. В отношении ли любых систем отсчета выполняется это утверждение?
Опыт показывает, что нет. Относительно ускоренно движущихся систем оно не выполняется (в качестве примера рассмотрите поведение мяча, лежащего на полу вагона, движущегося с ускорением). Обобщив подобные опыты, Исаак Ньютон и сформулировал первый закон динамики.
Первый закон Ньютона: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет скорость постоянной, если на него не действуют другие тела (или их действие компенсируется):
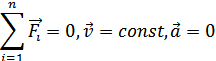
Первый закон Ньютона выполняется в инерциальных системах отсчета.
2. Инерциальная система отсчета
Системы отсчета, относительно которых тело при компенсации внешних воздействий движется равномерно и прямолинейно, называются инерциальными системами.
При рассмотрении явлений, на которые не влияет вращение Земли вокруг своей оси и ее движение вокруг Солнца, систему, связанную с Землей (геоцентрическая система), можно считать инерциальной.
Если же необходимо учитывать движение Земли, то инерциальной считают систему, связанную с Солнцем (гелиоцентрическая система).
Если же известна хотя бы одна инерциальная система, то инерциальными будут все другие системы отсчета, движущиеся относительно ее прямолинейно и равномерно.
3. Принцип относительности Галилея
Проведем опыт, например, будем бросать мяч вертикально вверх в вагоне, движущемся равномерно и прямолинейно, и на платформе. В обоих случаях будем видеть одно и то же: сначала мяч движется замедленно вверх, затем ускоренно вниз и падает обратно в руки.
Это показывает, что никакими механическими опытами, проводимыми в данной системе отсчета, нельзя установить, движется ли она равномерно и прямолинейно или находится в покое (рис. 3.1, а, б).
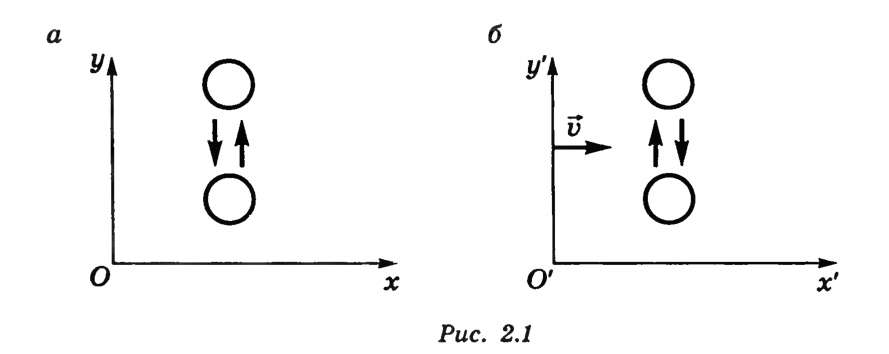
Рис. 3.1. Движение мяча а) относительно платформы, б) относительно вагона поезда.
Это объясняется тем, что во всех инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях (принцип относительности Галилея).
4. Масса
При воздействии одних тел на другие тела изменяют свою скорость — приобретают ускорение. При этом разные тела при данном воздействии приобретают разное ускорение (т. е. оказывают разное сопротивление изменению их скоростей).
Свойство тел приобретать определенное ускорение при данном воздействии называется инертностью. Инертность состоит в том, что для изменения скорости тела на заданную величину нужно, чтобы на него действовало другое тело и это действие длилось некоторое время.
Инертность — это свойство, присущее всем телам. Масса тела — количественная мера его инертности.
О теле, которое в результате взаимодействия меньше изменяет свою скорость, говорят, что оно более инертно, масса его больше:
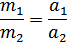
В СИ единицей массы тела является килограмм (кг).
Так как масса входит в закон всемирного тяготения, то она определяет также гравитационное взаимодействие тел.
Установленная теорией относительности взаимосвязь между массой и энергией
W = mс2
показывает, что масса является мерой полной энергии тел.
Масса тела обладает свойством аддитивности (сложения): при соединении двух тел в одно массы этих тел складываются. Свойство аддитивности массы очень точно выполняется для макроскопических тел и нарушается лишь тогда, когда энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в атомное ядро.
Существуют два основных способа определения массы тела:
1)путем сравнения ускорений тела неизвестной массы и эталона массы при их взаимодействии
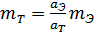 ;
;
2) путем взвешивания на рычажных весах.
В классической механике Ньютона считают, что:
1. масса тела не зависит от скорости его движения;
2. масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит;
3. для данной системы тел выполняется закон сохранения массы: при любых процессах, происходящих в системе тел, ее масса остается неизменной.
5.Сила
При действии на тело других тел может изменяться либо форма и размеры тела (тело деформируется), либо скорость тела (тело приобретает ускорение), либо возможно одновременно и то, и другое.
Физическая величина, описывающая и измеряющая воздействие одного тела на другое, в результате которого тела приобретают ускорения или деформируются, называется силой.
Сила F — величина векторная. Она характеризуется модулем, точкой приложения и направлением в пространстве.
Точку приложения силы в твердом теле можно переносить только вдоль линии ее действия ОО', не изменяя результата ее действия на тело (рис. 5.1).
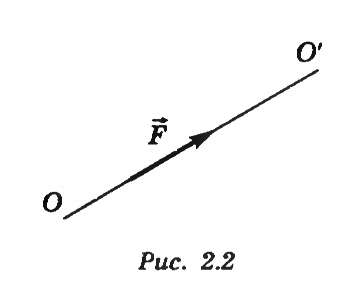
Рис. 5.1. Линия, вдоль которой можно переносить точку приложения силы.
В механике изучают силу упругости, силу трения, силу тяжести, силу тяготения.
Единицей измерения силы в СИ является ньютон (Н). Обычно для измерения силы пользуются динамометром.
Закон установлен на основании обобщения многочисленных опытов и наблюдений. Проиллюстрировать его можно с помощью опыта, схема которого изображена на рисунке 6.1.
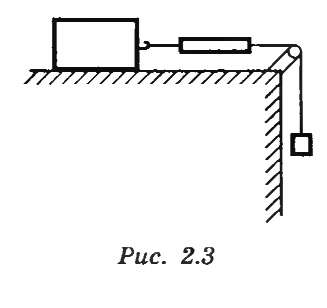
Рисунок 6.1. Схема опыта, иллюстрирующего второй закон Ньютона.
Второй закон Ньютона. Ускорение тела прямо пропорционально силе, действующей на тело, обратно пропорционально массе этого тела и направлено в сторону действия силы:
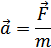
Если на тело действуют несколько сил, то, как показывает опыт, выполняется принцип независимости действия сил. Каждая сила сообщаетсвое ускорение. Результирующее ускорение
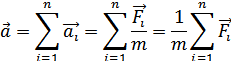
Где
Более полная формулировка второго закона Ньютона: ускорение тела прямо пропорционально равнодействующей всех сил, действующих на тело, обратно пропорционально массе тела и направлено в сторону равнодействующей силы.
Второй закон Ньютона выполняется в инерциальных системах отсчета.
Важно понять: из второго закона Ньютона следует, что сила определяет направление ускорения, а не направление скорости:
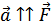
Так, например, под действием силы тяжести тело может двигаться вертикально вниз (рис. 6.2, а) и по параболе (рис. 6.2, б).
Рисунок 6.2. Движение тела под действием силы тяжести а) вниз, б) по параболе.
Опыт показывает, что действие тел друг на друга является двусторонним. Нельзя обнаружить такого случая, чтобы какое-то тело действовало на другое тело и не испытывало бы при этом ответного действия.
Третий закон Ньютона: силы, с которыми взаимодействуют два тела, одной природы, равны по модулю, направлены вдоль одной прямой в противоположные стороны и приложены к разным телам:
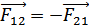
Силы взаимодействия возникают одновременно и попарно. Так как они приложены к разным телам, то не могут уравновешивать друг друга.
Следует иметь в виду, что третий закон справедлив независимо от того, покоятся ли взаимодействующие тела или же они движутся, находятся они в непосредственном контакте друг с другом или разделены пространством.
Рассмотрим следующие примеры:
1.Книга лежит на столе. Со стороны стола действует сила реакции 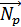 со стороны книги — ее вес
со стороны книги — ее вес 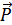 .
.
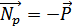
Вес книги приложен к столу, сила реакции опоры — к книге (рис. 7.1).
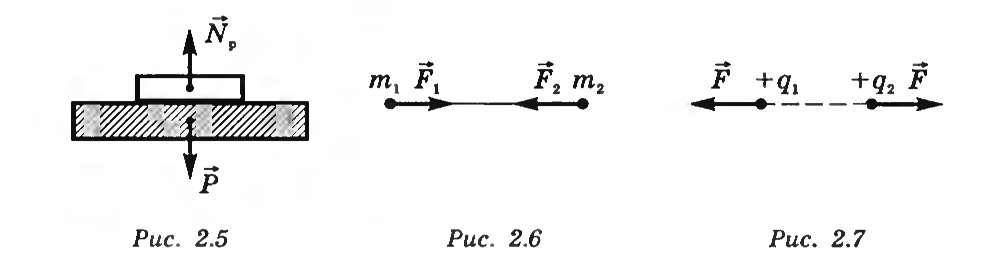
Рисунок 7.1. Силы, действующие на книгу, лежащую на столе.
2. Две материальные точки массами m1 и m2 притягиваются друг к другу, находясь на расстоянии r (рис. 7.2).

Рисунок 7.2. Силы, действующие на материальные точки при притяжении.
3. Два маленьких одноименно заряженных шарика взаимодействуют друг с другом с силами отталкивания (рис. 7.3).

Рисунок 7.3. Взаимодействие одноименно заряженных тел.
8. Силы упругости
Изменения формы и размеров тела называют деформациями.
Деформация — результат движения частей тела относительно друг друга. Деформации могут быть вызваны действием на тело внешних сил. Различают деформации растяжения (сжатия), изгиба, сдвига (среза), кручения (рис. 8.1).
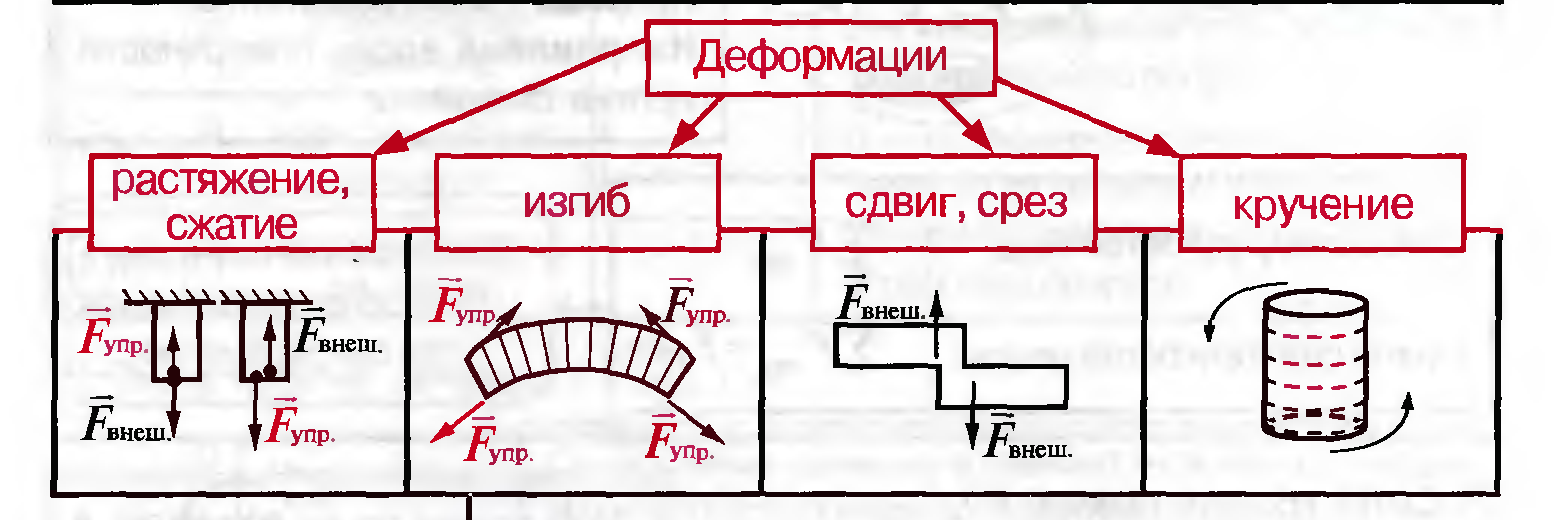
Рисунок 8.1. Виды деформации.
Деформации, полностью исчезающие после прекращения действия на тело сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, — пластическими.
Способность к упругим и пластическим деформациям зависит от природы вещества, из которого изготовлено тело, от условий, в которых оно находится, от способа его изготовления.
При деформации твердого тела происходит смещение частиц (атомов, молекул, ионов) из первоначальных положений равновесия в новые положения. При этом изменяются силовые взаимодействия между отдельными частицами тела. В результате в деформированном теле возникают внутренние силы, препятствующие его деформации.
Силы, возникающие в теле при его упругой деформации и направленные в сторону, противоположную смещению частиц при деформации, называют силами упругости.
Силы упругости препятствуют изменению размеров и формы тела. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации.
Силы упругости перпендикулярны поверхности соприкосновения взаимодействующих тел, а если во взаимодействии участвуют такие тела, как пружины, нити, то силы упругости направлены вдоль их оси.
Силу упругости, действующую на тело со стороны опоры, часто называют реакцией опоры (N), силу упругости, действующую со стороны подвеса, называют силой натяжения (T) (рис. 8.2).
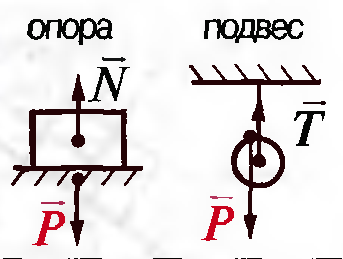
Рисунок 8.2 Сила реакции опоры и сила натяжения
Природа упругих сил электромагнитная.
9. Закон Гука
Линейная деформация (деформация растяжения) — деформация, при которой происходит изменение только одного линейного размера тела. Количественно она характеризуется абсолютным Δ l и относительным ε удлинением.
Абсолютное удлинение:
х = Δ l = l — l0
где l и l0 — длины тела в деформированном и недеформированном состояниях соответственно (рис. 9.1).
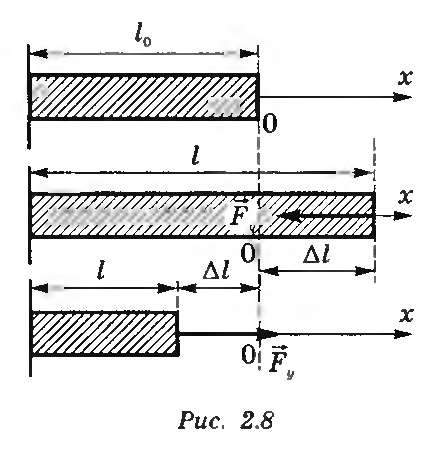
Рисунок 9.1. Удлинение стержня при деформации.
Относительное удлинение
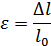
Небольшие и кратковременные деформации с достаточной степенью точности могут рассматриваться как упругие. Для таких деформаций Роберт Гук экспериментально установил закон.
Закон Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную направлению смещения частиц тела •
Fx=-kx
Здесь Fx — проекция силы на ось Ох, k — жесткость тела, зависящая от размеров тела и материала, из которого оно изготовлено.
Жесткость численно равна силе упругости, возникающей в теле при единичном абсолютном удлинении.
В СИ единицей жесткости является ньютон на метр  .
.
Графически зависимость Fx=f(x) представлена на рисунке 9.2.
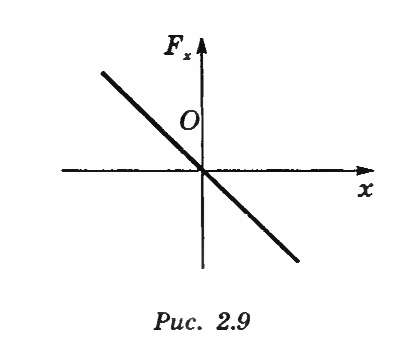
Рисунок 9.2. Зависимость Fx=f(x)
На законе Гука основано действие динамометра – прибора, предназначенного для измерения сил.
На практике часто трудно определить величину деформации, так как она мала.
10. Силы трения. Коэффициент трения
Силой трения называют силу, возникающую при соприкосновении двух тел и препятствующую их относительному перемещению. Она приложена к телам вдоль поверхности соприкосновения. Трение, возникающее между поверхностями различных тел, называют внешним трением. Если трение проявляется между частями одного и того же тела, то оно называется внутренним трением.
Трение между поверхностями двух соприкасающихся твердых тел при отсутствии между ними жидкой или газообразной прослойки называется сухим трением.
Трение между поверхностью твердого тела и окружающей его жидкой или газообразной средой, в которой тело движется, называется вязким трением.
Различают трение покоя, трение скольжения и трение качения.
Сила трения покоя Fтр.п. возникает между неподвижными твердыми телами, когда есть силы, действующие в направлении возможного движения тела.
Сила трения покоя всегда равна по модулю и направлена противоположно силе, параллельной поверхности соприкосновения и стремящейся привести это тело в движение. Увеличение этой приложенной к телу внешней силы приводит к возрастанию и силы трения покоя. Сила трения покоя направлена в сторону, противоположную возможному перемещению тела (рис. 10.1 а, б).
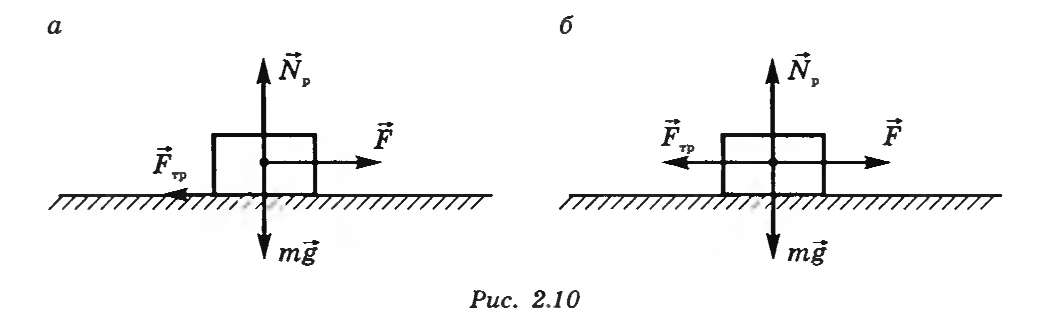
Рисунок 10.1. Изображение силы трения.
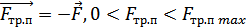
Максимальная сила трения покоя пропорциональна модулю силы нормального давления FД, производимого телом на опору:
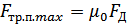
Так как по третьему закону Ньютона
FД=Np
Np — сила нормальной реакции опоры, то
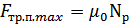
Здесь 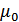 — коэффициент трения покоя, зависящий от материала и состояния трущихся поверхностей. Сила трения покоя препятствует началу движения. Но бывают случаи, когда сила трения покоя служит причиной возникновения движения тела. Например, ходьба человека. При ходьбе сила трения покоя, действующая на подошву, сообщает нам ускорение. Подошва не скользит назад, и, значит, трение между ней и дорогой — это трение покоя.
— коэффициент трения покоя, зависящий от материала и состояния трущихся поверхностей. Сила трения покоя препятствует началу движения. Но бывают случаи, когда сила трения покоя служит причиной возникновения движения тела. Например, ходьба человека. При ходьбе сила трения покоя, действующая на подошву, сообщает нам ускорение. Подошва не скользит назад, и, значит, трение между ней и дорогой — это трение покоя.
Рассмотрим брусок, лежащий на тележке(рис. 10.2).
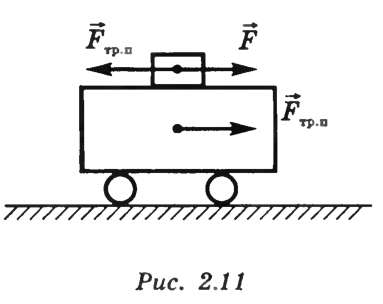
Рисунок 10.2. Силы, действующие на брусок.
На него действует сила F, стремящаяся сдвинуть его с места. В противоположном направлении на брусок со сторонытележки действует сила трения покоя 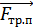 . На тележку со стороны бруска действует такая же по модулю и противоположная по направлению сила
. На тележку со стороны бруска действует такая же по модулю и противоположная по направлению сила 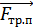 , приводящая к движению тележки вправо.
, приводящая к движению тележки вправо.
Сила трения покоя играет принципиальную роль в движении машин. Шины ведущих колес автомобилей как бы отталкиваются от дороги, и при отсутствии пробуксовки толкающая автомобиль сила — это сила трения покоя.
Также сила трения покоя препятствует скольжению тела, находящегося на наклонной плоскости (рис.10.3).
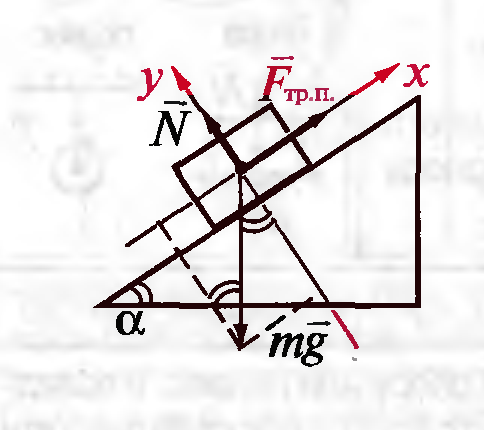
Рисунок 10.3. Тело, находящееся на наклонной плоскости.
Сила трения скольжения FTp возникает при соприкосновении движущихся относительно друг друга тел и затрудняет их движение. Сила трения скольжения направлена вдоль поверхности соприкосновения в сторону, противоположную скорости движения. Сила трения скольжения прямо пропорциональна силе нормального давления:
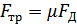 =>
=> 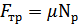 .
.
где 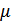 — коэффициент трения скольжения, зависящий от качества обработки поверхностей и их материала.
— коэффициент трения скольжения, зависящий от качества обработки поверхностей и их материала.
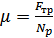 — const для данных тел.
— const для данных тел.
μ0>μ— сдвинуть тело с места труднее, чем продолжать его начавшееся скольжение.
Сила трения не зависит от площади соприкасающихся поверхностей тел и их положения относительно друг друга, а также от модуля скорости при небольших скоростях, но зависит от направления скорости: при изменениинаправления скорости изменяется и направление FTp (рис. 10.4).
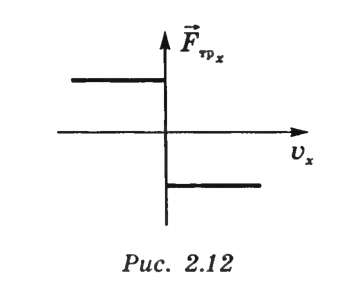
Рисунок 10.4. Зависимость направления силы трения от направления скорости.
Действие сил трения скольжения сопровождается превращением механической энергии во внутреннюю.
Существование сил трения объясняется проявлением сил электромагнитного взаимодействия. Силы трения покоя вызываются в основном упругими деформациями микровыступов на поверхности трущихся тел, силы трения скольжения возникают в результате пластических деформаций микровыступов и их частичного разрушения, а также сил межмолекулярного взаимодействия в области контактов (рис.10.5).
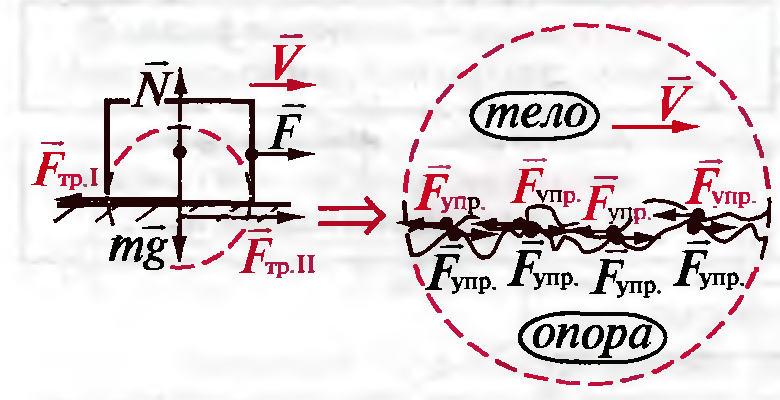
Рисунок 10.5. Причины возникновения силы трения.
11. Движение тела с учетом силы трения
Сила трения скольжения всегда направлена в сторону, противоположную скорости движения. Поэтому ускорение, сообщаемое силой трения, противоположно скорости (рис.11.1)
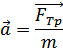
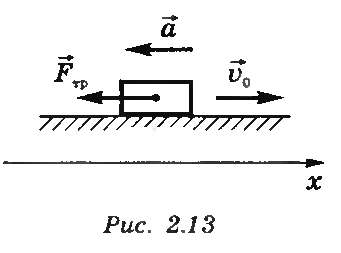
Рисунок 11.1. Схематическое изображение векторов.
Следовательно, действие силы трения приводит к уменьшению модуля скорости. Если на тело действует только FTр, то оно обязательно остановится, пройдя некоторое расстояние — тормозной путь. Рассчитаем его.
При равнозамедленном движении проекция перемещения
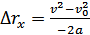 .
.
Так как
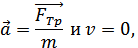
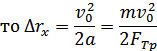
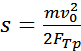 — тормозной путь.
— тормозной путь.
s ~ 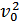 ! Об этом нужно помнить водителям машин и пешеходам, пересекающим улицу.
! Об этом нужно помнить водителям машин и пешеходам, пересекающим улицу.
12. Гравитационные силы. Закон всемирного тяготения
Все тела в природе взаимно притягиваются друг к другу. Впервые Ньютон доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения (гравитационная сила), действующая между любыми телами Вселенной.
Гравитационные силы — это силы центральные, т. е. они направлены вдоль прямой, соединяющей взаимодействующие материальные точки.
Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это поле, наряду с другими полями и веществом, является одной из форм материи.
С каждым телом неразрывно связано гравитационное поле, проявляющееся в том, что на помещенную в поле материальную точку действует гравитационная сила, пропорциональная массе этой точки.
Тело, гравитационное поле которого исследуется, называется источником поля.
Гравитационные силы зависят от положения тел (координат) (рис. 12.1).
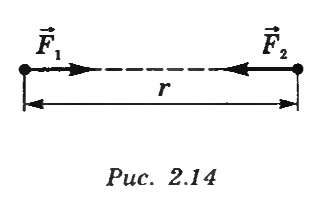
Рисунок 12.1. Силы гравитационного взаимодействия.
Их просто рассчитать для материальных точек по закону всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
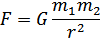
G = 6,67-10-11 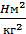 — гравитационнаяпостоянная.
— гравитационнаяпостоянная.
Гравитационная постоянная определена опытным путем. Она численно равна силе, с которой притягиваются два тела массами 1 кг, находящиеся на расстоянии 1 м друг от друга.
По закону всемирного тяготения можно рассчитать также силу притяжения между двумя сферическими телами (r — это расстояние между центрами сфер) или телами, одно из которых — шар большого радиуса, а второе — произвольной формы, но небольших размеров (рис. 12.2, а, б).
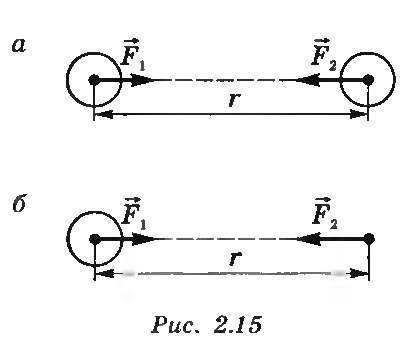
Рисунок 12.2 Гравитационное взаимодействие между а) двумя сферическими телами, б) сферическим телом и материальной точкой.
13. Сила тяжести
Сила тяжести — это сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения:
FT = mg.
Любое тело, находящееся на Земле (или вблизи нее), вместе с Землей вращается вокруг ее оси, т. е. тело движется по окружности радиусом r с постоянной по модулю скоростью (рис. 13.1).
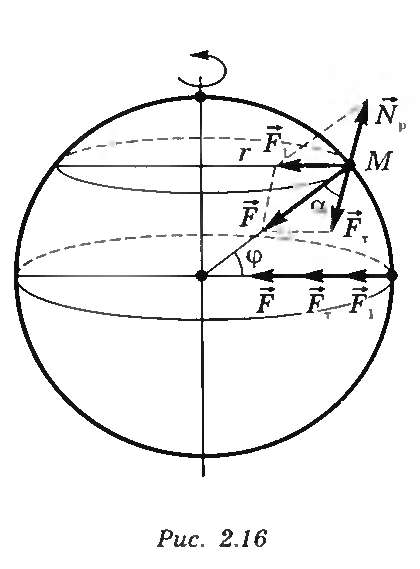
Рисунок 13.1. Силы, действующие на тело на поверхности Земли.
На тело на поверхности Земли действуют сила тяготения F и сила со стороныземной поверхности Np. Их равнодействующая
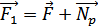 (13.1)
(13.1)
сообщает телу центростремительное ускорение
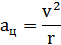
Разложим силу тяготения F на две составляющие, одна из которых будет F1, т. е.
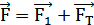 . (13.2)
. (13.2)
Из уравнений (13.1) и (13.2) видим, что
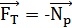
Таким образом, сила тяжести FT — одна из составляющих силы тяготения. Вторая составляющая 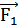 сообщает телу центростремительное ускорение.
сообщает телу центростремительное ускорение.
В точке М на географической широте φ сила тяжести направлена не по радиусу Земли, а под некоторым углом α к нему. Сила тяжести направлена по так называемой отвесной прямой (по вертикали вниз).
Сила тяжести равна по модулю и направлению силе тяготения только на полюсах. На экваторе они совпадают по направлению, а по модулю отличие наибольшее.
FT=F-F1,FT=F-mω2R
где ω — угловая скорость вращения Земли, R — радиус Земли.
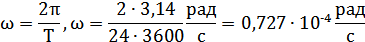
Так как ω очень мала, то FT≈ F. Следовательно, сила тяжести мало отличается по модулю от силы тяготения, поэтому данным различием часто можно пренебречь.
Тогда
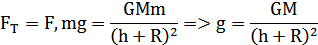
Из этой формулы видно, что ускорение свободного падения g не зависит от массы падающего тела, но зависит от высоты.
14. Движение тела под действием силы тяжести
Если на тело действует только сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости. При этом возможны следующие случаи движения тела:
· Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное свободное падение.
· Если начальная скорость тела направлена под углом к силе тяжести, то тело будет двигаться по параболе, либо по ветви параболы.
· Тело может двигаться по круговой или эллиптической орбите вокруг планеты.
15. Вес тела
Весом тела называется сила, с которой тело действует на неподвижную относительно него опору или подвес.
Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы реакции) или подвеса (силы натяжения) Вес существенно отличается от силы тяжести:
1. Это силы разной природы: сила тяжести — гравитационная сила, вес — упругая сила (электромагнитной природы).
2. Они приложены к разным телам: сила тяжести — к телу, вес — к опоре (рис. 15.1).
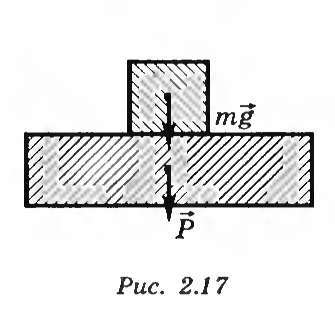
Рисунок 15.1. Схематическое изображение силы тяжести и веса тела.
3. Направление веса тела не обязательно совпадает с отвесным направлением.
4. Сила тяжести тела в данном месте Земли постоянная и не зависит от характера движения тела; вес зависит от ускорения, с которым движется тело.
Рассмотрим, как изменяется вес тела, движущегося в вертикальном направлении вместе с опорой (рис. 15.2 а, б, в). На тело действуют силатяжести FT = mg и сила реакции опоры Np.
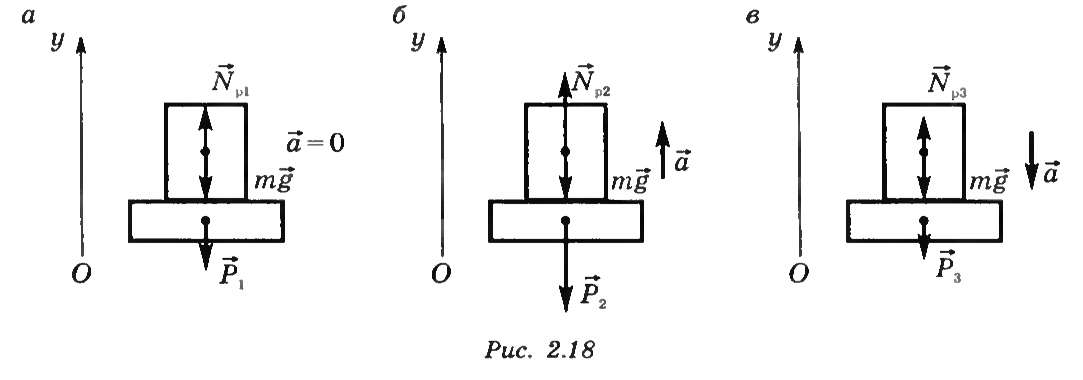
Рисунок 15.2. движение тела вместе с опорой а) равномерно, б) ускоренно вверх, в) ускоренно вниз.
Основное уравнение динамики:
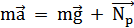 .
.
В проекции на ось Оу:
а) 0 = Npl - mg => Npl = mg.
По третьему закону Ньютона модули сил Np1 = P1. Следовательно, вес тела
P1 = mg.
б) mа = Np2 - mg => Np2=m(a + g).
Значит,
P2=m(a + g) => Р2> mg
тело испытывает перегрузки.
в) -ma = Np3-mg => Np3=m(g-a).
Следовательно, вес тела
P3=m(g-a) => P3<mg.
Если a-g, то Р = 0.
Таким образом, вес тела при вертикальном движении может быть в общем случае выражен формулой
P = m(g±a).
16. Невесомость
Мысленно разобьем неподвижное тело на горизонтальные слои. На каждый из этих слоев действует сила тяжести mg и вес Р вышележащей части тела (рис. 16.1). Этот вес будет становиться тем больше, чем ниже лежит слой. Поэтому под влиянием веса вышележащих частей тела каждый слой деформируется и в нем возникают упругие напряжения, которые возрастают по мере перехода от верхней части тела к нижней.
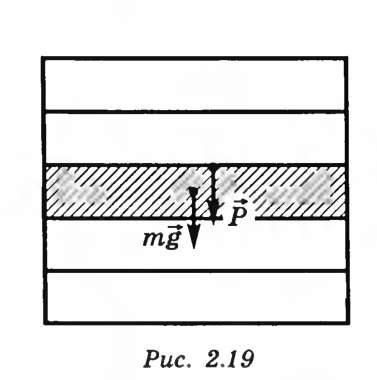
Рисунок 16.1 Давление верхних слоев тела на нижние.
Если тело свободно падает (a = g), то его вес равен нулю, в теле исчезают всякие деформации и, несмотря на сохраняющееся действие силы тяжести, верхние слои не будут давить на нижние.
Состояние, при котором в свободно движущемся теле исчезают деформации и взаимные давления, называется невесомостью.
Причина невесомости заключается в том, что сила всемирного тяготения сообщает телу и его опоре одинаковое ускорение.
17. Первая космическая скорость
Первая космическая скорость для данной планеты — это скорость, которую надо сообщить телу при запуске, чтобы оно стало спутником планеты и при этом двигалось по круговой орбите вблизи ее поверхности.
Пусть искусственный спутник находится на высоте h над поверхностью планеты. Сила тяготения сообщает спутнику центростремительное ускорение (рис. 17.1).
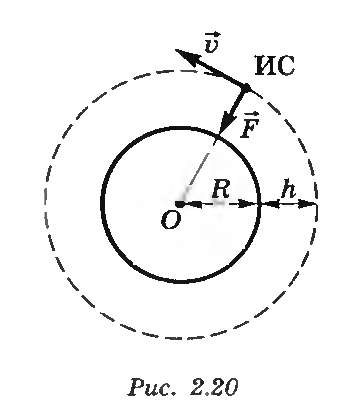
Рисунок 12.1. Круговая орбита вращения ИС.
По второму закону Ньютона
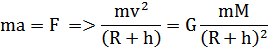
следовательно,линейная скорость спутника движущегося по круговой орбите (круговая скорость) на высоте h над поверхностью планеты:
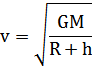
Здесь G — гравитационная постоянная, М — масса планеты, R — ее радиус.
Вблизи планеты (h = 0) первая космическая скорость:
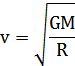
Так как вблизи Земли
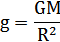
то первая космическаяcкорость для Земли 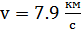
18. Движение искусственных спутников
Для того чтобы тело стало искусственным спутником, его надо поднять на некоторую высоту (вывести на орбиту) и сообщить ему горизонтальную относительно поверхности Земли скорость (рис. 18.1).
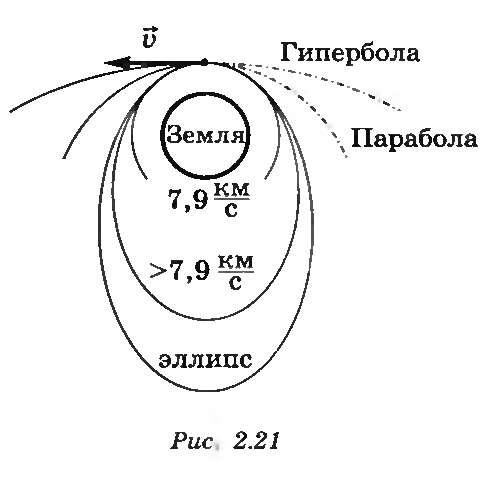
Рисунок 18.1. Форма траектории при движении ИС.
Для запуска используют ракеты. После вывода на орбиту ракета разгоняет спутник до требуемой скорости, после этого спутник отделяется от ракеты-носителя и продолжает свое движение по орбите только под действием силы тяготения. Если спутнику вблизи Земли сообщить скорость 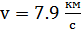 , то он будет двигаться по круговой орбите.
, то он будет двигаться по круговой орбите.
Если 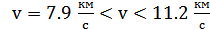 , то спутник будет двигаться по эллиптической орбите.
, то спутник будет двигаться по эллиптической орбите.
Скорость, которую надо сообщить телу, чтобы оно, преодолев притяжение планеты, стало спутником Солнца, называют второй космической скоростью.
Для Земли вторая космическая скорость
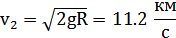
Развив скорость 11,2 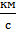 , тело начинает двигаться по параболе. Если
, тело начинает двигаться по параболе. Если 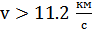 то тело движется по гиперболе.
то тело движется по гиперболе.
Движение искусственных спутников планеты происходит под действием только одной силы — силы тяготения. Эта сила сообщает спутнику и всем находящимся на нем телам одинаковое ускорение — ускорение свободного падения. Поэтому все тела на спутниках находятся в состоянии невесомости.
19. Неинерциальные системы отсчета
Системы отсчета, в которых свободная материальная точка или свободное тело не сохраняют скорость движения неизменной при компенсации внешних воздействий (неинерциальное движение), называются неинерциальными системами отсчета (НСО).
Неинерциальной является система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета (ИСО).
В элементарном курсе физики рассматриваются простейшие неинерциальные системы отсчета, движущиеся поступательно с ускорением. В неинерциальных системах отсчета не выполняются законы Ньютона. Покой или движение материальных точек и тел в неинерциальных системах отсчета описываются уравнениями, аналогичными по форме записи уравнению второго закона Ньютона, однако в уравнение вводятся силы инерции.
Силы инерции не вызываются воздействиями на данную материальную точку или тело каких-то других тел или полей, они лишь отражают неинерциальность самой системы отсчета.
Силы инерции, прикладываемые к какой-либо системе материальных точек, нарушают замкнутость этой системы и всегда являются для этой системы внешними силами.
20. Явления, наблюдаемые в неинерциальных системах отсчета
При описании поступательного движения тела в неинерциальной системе отсчета (НСО), движущейся поступательно, вводится сила инерции
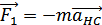 ,
,
где 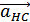 — ускорение самой НСО относительно какой-то инерциальной системы отсчета.
— ускорение самой НСО относительно какой-то инерциальной системы отсчета.
Рассмотрим пример с шаром массой m, находящимся на гладком полу вагонетки и прикрепленным к ее передней стенке пружиной (рис. 20.1).
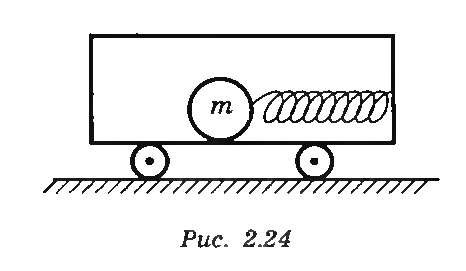
Рисунок 20.1. Шар прикреплен к стенке вагонетки пружиной.
На рисунке 20.2 система хОу — неподвижная инерциальная система отсчета, а х'О'у' — неинерциальная система отсчета, связанная с вагонеткой.
При движении вагонетки с ускорением 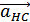 относительно хОу пружина растянется на Δ l, положение шара в начале движения относительно вагонетки изменится по сравнению с его положением при aHC=0, а далее относительно вагонетки он будет неподвижен.
относительно хОу пружина растянется на Δ l, положение шара в начале движения относительно вагонетки изменится по сравнению с его положением при aHC=0, а далее относительно вагонетки он будет неподвижен.
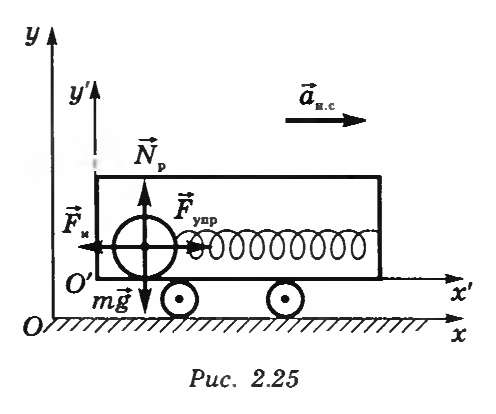
Рисунок 20.2. Изображение ИСО и НСО.
При отсутствии трения
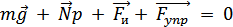 ,
,
где mg — сила тяжести, Np — сила реакции пола, Fynp — сила упругости со стороны растянутой пружины, FИ — сила инерции.
В проекциях на оси Оу и Ох имеем:
mg = Np; FИ =Fynp
Так как модуль Fynp= kΔ l, то FИ может быть измерена по растяжению пружины.
Движение шара вместе с вагонеткой относительно инерциальной системы хОу описывается вторым законом Ньютона:
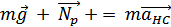 ,
,
или в проекции
Fynp=m 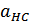 .
.
Тогда
FИ = 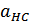 ,
,
а с учетом направлений
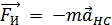
При решении задач по теме "Динамика материальной точки" следует придерживаться следующего алгоритма:
1. Сделать схематический рисунок, изобразив все силы, действующие на каждое тело рассматриваемой системы.
2. Выбрать систему координат хОу с таким расположением осей, чтобы наибольшее количество векторов сил было направлено вдоль осей. В случае движения тела по окружности ось Ох должна быть направлена к центру окружности (как и центростремительное ускорение).
3. Записать для каждого тела в отдельности второй закон Ньютона ввекторной форме (динамическое уравнение движения):
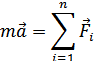
4. Спроецировать эти уравнения на выбранные оси координат.
5. Дополнить полученную систему в случае необходимости кинематическими и динамическими соотношениями и решить ее относительно искомой величины.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Автомобиль массой 3000 кг, разгоняясь из состояния покоя, достигает скорости 8,0 м/с, а затем продолжает движение с выключенным двигателем до полной остановки. Определите ускорения автомобиля при разгоне и при торможении, полное время движения и пройденный путь. Сила тяги двигателя 3000 Н, коэффициент сопротивления 0,020.
Дано: m = 3000 кг, v0=0, v1 = 8,0 м/с, v = 0, F=3000 Н, μ = 0,020.
Найти: а1, а2, t, s.
Решение. На автомобиль на разгонном участке действуют сила тяжести mg, сила нормальной реакции полотна дороги Np, сила тяги F, сила сопротивления Fc.
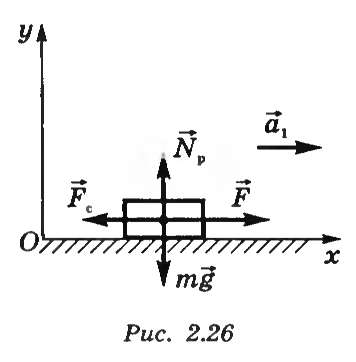
Запишем основное уравнение динамики в векторной форме:
m 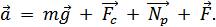
В проекциях на оси Ох и Оу:
ma1 = F -Fc; 0 = Np - mg.
Так как Fc =μNp, то, решая вместе эти уравнения, найдем ускорение а1:
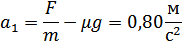
Путь, пройденный автомобилем при разгоне,найдем по формуле
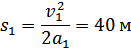
Запишем основное уравнение динамики для участка торможения:
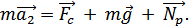
В проекциях на оси Ох и Оу:
mа2 = Fc; 0 = Np - mg.
Решая вместе эти уравнения, найдем ускорение а2:
а2 = μg= 0,20 м/с2.
Длина участка торможения
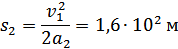
Пройденный путь
s = s1 + s2 = 2,0 102 м.
Полное время движения
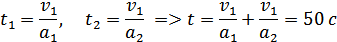
 2015-05-06
2015-05-06 7743
7743

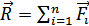 —
— 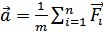 —
— 






