Зависимость между изгибающим моментом, поперечной
Построение эпюр поперечних сил и изгибающих моментов.
Лекция 7
Рассмотрим балку, нагруженную произвольной распределенной нагрузкой 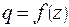 (рис. 7.1,а).
(рис. 7.1,а).
Выделим из бруса элемент длиной 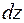 и приложим слева и справа поперечные силы
и приложим слева и справа поперечные силы  и(
и( +
+ 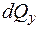 ) и изгибающие моменты
) и изгибающие моменты и (
и ( +
+ 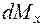 ), соответственно, приняв направления этих силовых факторов положительными в соответствии с выбранными выше правилами знаков (рис. 7.1,б). В пределах малого участка
), соответственно, приняв направления этих силовых факторов положительными в соответствии с выбранными выше правилами знаков (рис. 7.1,б). В пределах малого участка 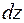 нагрузку
нагрузку 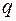 принимаем распределенную равномерно.
принимаем распределенную равномерно.
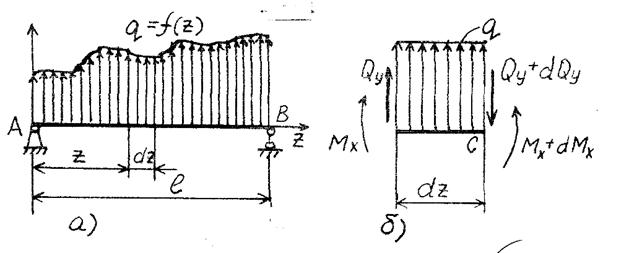
Рис. 7.1
Составим уравнения равновесия:
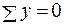 ;
; 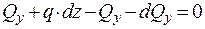 ;
;
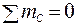 ;
; 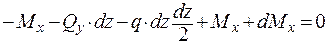 .
.
Произведя упрощения и отбросив произведение величин высшего порядка малости, получим 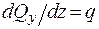 , т.е. первая производная от поперечной силы по длине балки равна интенсивности распределенной нагрузки;
, т.е. первая производная от поперечной силы по длине балки равна интенсивности распределенной нагрузки; 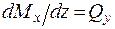 из второго уравнения, т.е. первая производная от изгибающего момента по длине балки равна поперечной силе.
из второго уравнения, т.е. первая производная от изгибающего момента по длине балки равна поперечной силе.
Эти соотношения действительны, когда абсцисса поперечного сечения балки возрастает от левого конца балки.
Полученные зависимости позволяют получить при любой внешней нагрузке следующиеправила проверки эпюр и
и :
:
1. На участках балки, где 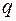 = 0, эпюры
= 0, эпюры ограничены прямыми, параллельными базе (продольной оси балки), а эпюра
ограничены прямыми, параллельными базе (продольной оси балки), а эпюра  – наклонными прямыми. 2. На участках, где
– наклонными прямыми. 2. На участках, где 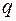 ¹0, эпюры
¹0, эпюры  ограничены прямыми, наклонными к базе, а эпюры
ограничены прямыми, наклонными к базе, а эпюры  – параболами, направленными 6 выпуклостью навстречу действию
– параболами, направленными 6 выпуклостью навстречу действию 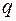 . 3. В сечениях балки, где эпюра
. 3. В сечениях балки, где эпюра меняет знак (слева направо) с (+) на (-), на эпюре
меняет знак (слева направо) с (+) на (-), на эпюре  экстремум максимум и наоборот... 4. На участках балки, где эпюра
экстремум максимум и наоборот... 4. На участках балки, где эпюра = 0, эпюра
= 0, эпюра  – прямая, параллельная базе. 5. На участках балки, где эпюра
– прямая, параллельная базе. 5. На участках балки, где эпюра > 0, эпюра
> 0, эпюра  возрастает слева направо, и наоборот.... В сечениях балки, где приложены внешние активные и реактивные сосредоточенные силы, на эпюре
возрастает слева направо, и наоборот.... В сечениях балки, где приложены внешние активные и реактивные сосредоточенные силы, на эпюре возникают скачки на их величину и в направлении этих сил, а на эпюре
возникают скачки на их величину и в направлении этих сил, а на эпюре – изломы, направленные навстречу этим силам. 7. В сечениях балки, где приложены сосредоточенные моменты, на эпюре
– изломы, направленные навстречу этим силам. 7. В сечениях балки, где приложены сосредоточенные моменты, на эпюре  возникают скачки на их величину и в направлении этих моментов. 8. Эпюра
возникают скачки на их величину и в направлении этих моментов. 8. Эпюра  является диаграммой производной от эпюры
является диаграммой производной от эпюры  . Следовательно, ордината на эпюре
. Следовательно, ордината на эпюре  в любом сечении равна тангенсу угла наклона касательной к эпюре
в любом сечении равна тангенсу угла наклона касательной к эпюре  в этом сечении балки.
в этом сечении балки.
Рассмотрим несколько примеров.
7.2. Пример 1. Построить эпюры  и
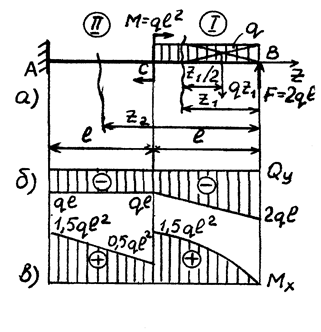
и  для консольной балки (рис. 7.2,а). Чтобы не определять реакции в опоре
для консольной балки (рис. 7.2,а). Чтобы не определять реакции в опоре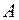 , строим эпюры от правого конца балки в следующем порядке. Разобьем балку
, строим эпюры от правого конца балки в следующем порядке. Разобьем балку 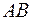 на участки I и II, в пределах которых законы изменения
на участки I и II, в пределах которых законы изменения  и
и  остаются постоянными. Границами участков являются: начало и конец балки, точки приложения внешних сосредоточенных сил (включая опорные реакции), начало и конец приложения распределенных сил
остаются постоянными. Границами участков являются: начало и конец балки, точки приложения внешних сосредоточенных сил (включая опорные реакции), начало и конец приложения распределенных сил 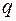 . Выберем начало координат на правом конце балки
. Выберем начало координат на правом конце балки 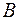 и на основании формул и правил знаков, составим выражения для
и на основании формул и правил знаков, составим выражения для  и
и  в произвольных сечениях
в произвольных сечениях 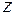 для каждого участка. Участок I
для каждого участка. Участок I 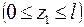 :
:
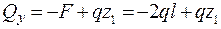 ;
; 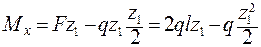 ;
;
здесь 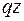 – равнодействующая распределенной нагрузки
– равнодействующая распределенной нагрузки 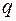 в пределах отрезка длиной
в пределах отрезка длиной 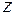 ; она приложена посредине этого отрезка и поэтому момент её отнсительно сечения
; она приложена посредине этого отрезка и поэтому момент её отнсительно сечения 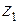 равен
равен 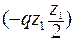 .
.
 При
При 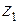 = 0;
= 0;  =
= 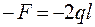 ;
;
 = 0;
= 0;
при 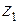 =
= 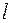 ;
; 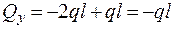 ;
;  =
= 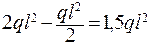 .
.
Участок II (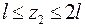 ):
): 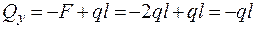 ,
,
т.е. поперечная сила на участке II не зависит от
на участке II не зависит от 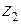 (конец приложения нагрузки
(конец приложения нагрузки 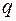 совпал с началом этого участка.
совпал с началом этого участка.
Рис.7.2 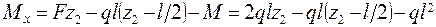 ;
;
при 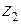 =
= 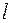 ;
; 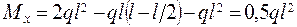 ;
;
при 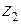 =
= 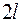 ;
; 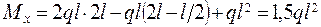 .
.
Выбрав масштаб, строим эпюры поперечных сил  и изгибающих моментов
и изгибающих моментов  (рис. 7.2.б,в), а затем проверяем правильность их получения.
(рис. 7.2.б,в), а затем проверяем правильность их получения.
7.3. Пример 2. Построить эпюры  и
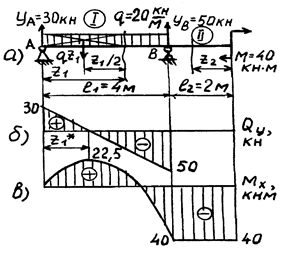
и  для двухопорной балки (рис. 7.3,а). Решение задачи:
для двухопорной балки (рис. 7.3,а). Решение задачи:
Определяем опорные реакции:
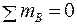 ;
; 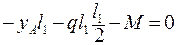 ;
;
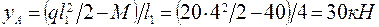 ;
;
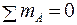 ;
; 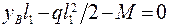 ;
;
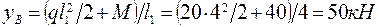 ;
;
Проверка: 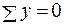 ;
; 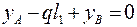 ; 30 – 20×4 + 50 = 0.
; 30 – 20×4 + 50 = 0.
Разбиваем балку на cиловые участки I и II; составляем выражения для и
и  :
:
Участок I (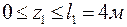 ):
):
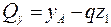 ;
; 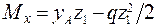 ;
;
при 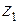 = 0;
= 0; 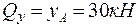 ;
;  = 0; при
= 0; при 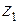 =
= 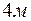 ;
;  = 30 – 20×4 = –50
= 30 – 20×4 = –50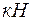 ;
;
 = 30×4 – 20×42/2 = –40
= 30×4 – 20×42/2 = –40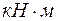 .
.
Построив эпюру видим,что
видим,что
она меняет знак c (+) на (-), т.е. на
участке I на эпюре необходимо определить экстремум.
необходимо определить экстремум.
Рис.7.3
Получим:
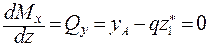 ;
;
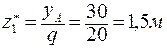 .
.
 Тогда:
Тогда: 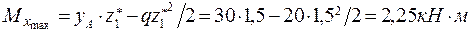 .
.
Участок II (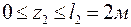 ):
): = 0;
= 0;  =
= 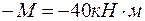 .
.
Эпюры  и
и  показаны на рис. 7.3 б, в.
показаны на рис. 7.3 б, в.
 2014-02-09
2014-02-09 1054
1054