Нормальных напряжений при чистом изгибе балки
Лекция 8
Рассмотрим консольную балку* произвольного поперечного сечения, постоянного по длине, нагруженную в вертикальной плоскости моментом  (рис. 7.8,а). При такой нагрузке
(рис. 7.8,а). При такой нагрузке  = 0, а
= 0, а  =
=  .
.
При прямом чистом изгибе балки справедливы:
1. Гипотеза плоских сеченийБернулли– сечения плоские и нормальные к оси балки до деформации остаются плоскими и нормальными к ее оси и после деформации.
2. Гипотеза о ненадавливаемости волокон: нормальные напряжения в продольных сечениях балки не возникают.
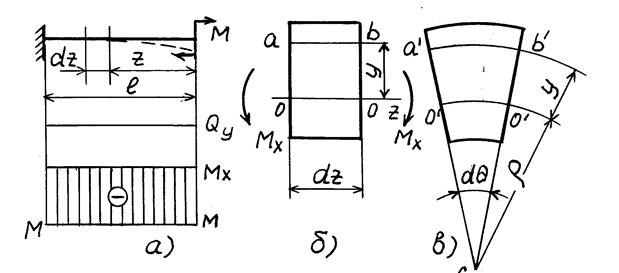 |
Рис. 8.1.
Т.к. поперечные силы = 0, то можно предположить, что не возникают в плоскости поперечных сечений и касательные напряжения.
= 0, то можно предположить, что не возникают в плоскости поперечных сечений и касательные напряжения.
Двумя поперечными сечениями  и
и 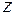 +
+ 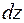 вырежем из балки элемент длиной
вырежем из балки элемент длиной 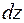 (рис.8.1,б). На его торцах возникнут изгибающие моменты
(рис.8.1,б). На его торцах возникнут изгибающие моменты  , которые вызовут деформацию изгиба (рис. 8.1,в): продольная ось
, которые вызовут деформацию изгиба (рис. 8.1,в): продольная ось  (волокно
(волокно 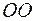 ) изогнется и получит радиус кривизны
) изогнется и получит радиус кривизны 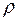 , длина же слоя
, длина же слоя 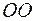 не изменится, т.е.
не изменится, т.е. 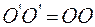 . Поперечные сечения при этом взаимно повернутся на угол
. Поперечные сечения при этом взаимно повернутся на угол 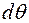 . Волокно
. Волокно 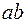 , расположенное на расстоянии
, расположенное на расстоянии 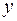 от продольной оси
от продольной оси 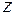 (от слоя
(от слоя 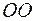 ), удлинится и займет положение
), удлинится и займет положение 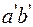 .
.
Относительное удлинение волокна 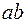 :
:
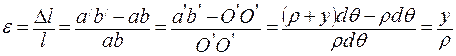 .
.
Т.к. каждое волокно согласно принятым выше гипотезам испытывает одноосное напряженное состояние, то, применив закон Гука, получим:
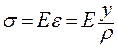 .
.
Таким образом, нормальные напряжения распределяются по линейному закону. Определим их из условия равновесия элемента балки. При равновесии должны соблюдаться шесть уравнений равновесия:
1. Т.к. внутренние силы 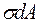 перпендикулярны осям
перпендикулярны осям 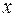 и
и 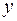 , то
, то 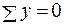 ;
; 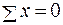 .
.
2. 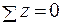 или
или 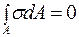 .
.
Получим
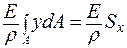 ,
,
но 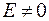 ;
; 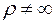 (ось балки изогнута). Следовательно,
(ось балки изогнута). Следовательно, 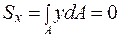 [м3].
[м3].
Статический момент площади 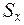 равен нулю относительно центральной оси. Следовательно, нейтральная ось при изгибе совпадает с центральной осью поперечного сечения.
равен нулю относительно центральной оси. Следовательно, нейтральная ось при изгибе совпадает с центральной осью поперечного сечения.
3. Уравнение 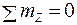 обращается в тождество, т.к. внутренние силы
обращается в тождество, т.к. внутренние силы 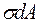 параллельны оси
параллельны оси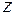 .
.
4. Уравнение 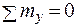 дает
дает 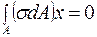 .
.
Получим
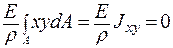 .
.
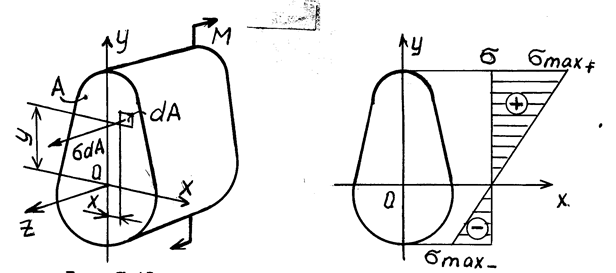
Рис. 8.2 Рис. 8.3
Т.к. 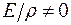 , то тогда центробежный момент инерции
, то тогда центробежный момент инерции 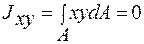 . Тогда
. Тогда 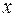 и
и 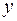 - главные оси сечения, а момент
- главные оси сечения, а момент  должен лежать в главной плоскости, что и выполняется. Отсюда следует: силовая линия и нейтральная ось взаимно перпендикулярны.
должен лежать в главной плоскости, что и выполняется. Отсюда следует: силовая линия и нейтральная ось взаимно перпендикулярны.
5. Приравниваем нулю сумму моментов сил относительно оси 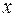 :
:
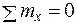 ;
; 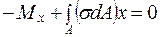 ; Получим:
; Получим:
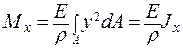 или
или 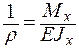 ,
,
где 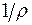 – кривизна нейтрального слоя балки;
– кривизна нейтрального слоя балки; 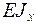 – жесткость поперечного сечения балки на изгиб относительно оси
– жесткость поперечного сечения балки на изгиб относительно оси 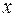 . Уравнение называютосновным уравнением изгиба.
. Уравнение называютосновным уравнением изгиба.
Получим искомую формулу:
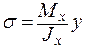 ,
,
где:  – внутренний изгибающий момент в сечении, в котором определяют
– внутренний изгибающий момент в сечении, в котором определяют 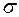 [Н×м];
[Н×м]; 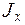 – осевой момент инерции поперечного сечения относительно нейтрального слоя [м4];
– осевой момент инерции поперечного сечения относительно нейтрального слоя [м4]; 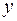 –расстояние от нейтрального слоя до слоя, в котором определяют напряжения [м].
–расстояние от нейтрального слоя до слоя, в котором определяют напряжения [м].
Эпюра нормальных напряжении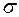 представлена на рис. 8.3. Наибольшие напряжения возникают в крайних волокнах, наиболее удаленных от нейтральной оси поперечного сечения балки.
представлена на рис. 8.3. Наибольшие напряжения возникают в крайних волокнах, наиболее удаленных от нейтральной оси поперечного сечения балки.
 2014-02-09
2014-02-09 3214
3214
