Введение понятия молекулярная фотоника принадлежит А.Н.Теренину

Гамильтониан молекулярной системы может быть представлен в виде суммы операторы кинетической энергии электронов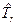, оператора кинетической энергии ядер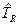, членов, описывающих кулоновское взаимодействие электронов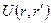, ядер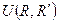, электронов и ядер между собой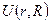и оператора спин-орбитального взаимодействия: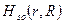

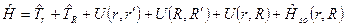, (1.1)

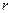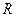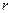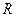где - обозначает набор координат электронов, а -набор координат ядер. Под и можно при этом понимать координаты, отсчитываемые от центра масс система, поскольку движение системы как целого всегда отделяется от относительных движений ее частей.*

Если кроме того произведено отделение колебательного движения ядер от вращательного движения молекулы (учет последнего необходим только для молекул в газовой фазе),координаты 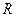соответствуют относительным колебательным координатам ядер. Кроме членов, указанных в (1.1) в выражение для молекулярного гамильтониана входит еще ряд малых членов (оператор спин-спинового взаимодействия электронов, электронов и ядер и др.), которые обычно несущественны для описания поведения электронно-возбужденных молекул, но учет которых необходим при описании магнитных эффектов.

Для молекул, не содержащих слишком тяжелых атомов,влияние спин- орбитального взаимодействия на положение электронных состояний мало. Поэтому на первом этапе рассмотрения оператор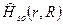

((подстрочное*⁾Хотя эта процедура неоднозначна [],члены зависящие от способа введения внутренних координат системы (так называемые масс-поляризационные члены),в случае многоатомной молекулы всегда малы,так как обратно пропорциональны массе всей молекулы и ими можно пренебречь.))

спин-орбитального взаимодействия можно опустить, учтя его влияние в дальнейшем с использованием теории возмущений. Собственные функции гамильтониана 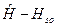могут быть в таком случае выбраны в виде собственных функций оператора квадрата полного электронного спинового момента молекулы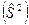 и оператора одной из его проекций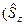обычно). Соответствующие состояния, называемые чисто спиновыми, классифицируются тогда по собственным значениям 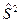и 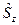. В большинстве молекул основное состояние является синглетным (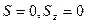).Электронно-возбужденные состояния могут быть как синглетными так и триплетными (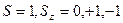). Триплетное состояние под действием спин-орбитального и спин-спинового взаимодействия и внешнего магнитного поля расщепляется на три подуровня в соответствии с тремя значениям .

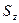Второе упрощение можно получить, если учесть, что массы ядер в тысячи раз превышают массу электрона. Это позволяет в качестве нулевого приближения рассматривать движение электронов, считая ядра покоящимися. Волновая функция электронов должна в таком случае находиться из электронного волнового уравнения с фиксированными значениям :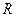

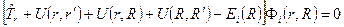(1.2)

где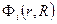- электронная волновая функция, параметрически зависящая от координат ядер, а 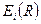- электронная энергия системы при некотором наборе координат ядер. Электронные волновые функции ортономированы. Член 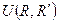входит в 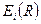в качестве аддитивного слагаемого. Индексом i обозначен набор электронных квантовых чисел. Функция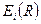определяет потенциальную поверхность (терм) электронного состояния i. Ее вид различен для различных электронных состояний.

Будем искать собственную функцию гамильтониана 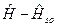в виде разложения:

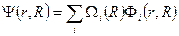. (1.3)

Подстановка (1.3) в уравнение Шредингера с гамильтонианом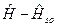, умножение его слева на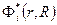и интегрирование по координатам электронов (что ниже обозначено угловыми скобками) дает уравнение

для определения коэффициентов разложения в 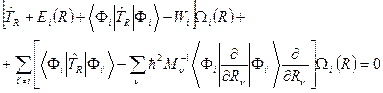(1.4)

Здесь использован явный вид оператора 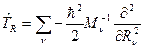, где 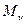-масса ядра .

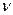Адиабатическое приближение или Борна [] состоит в том, что в уравнении (1.4)пренебрегается всеми недиагональными по i матричными элементами, но удерживается диагональный матричный элемент. Приближение, когда пренебрегается всеми матричными элементами, содержащие производные по координатам ядер, носит название Борна- Оппенгеймера. Точность приближения Б.-О. оценивалась для молекулы Н₂ Колосом и Вольневичем и составляет ~10^-2%.

Волновая функция системы в этом приближении имеет вид произведения

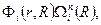где ядерные волновые функции 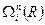определяются уравнением (1.4), в котором опущены недиагональные по i члены, В качестве потенциальной энергии движения ядер в этом уравнении фигурирует сумма электронной энергии 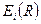и (малого) члена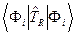, описывающего влияние движения ядер на потенциальную поверхность в адиабатическом приближении. Индексом n обозначен набор квантовых чисел, нумерующих состояния ядерной подсистемы в данном электронном состоянии.

Для связывающего электронного терма состояния с энергией 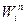будут колебательными состояниями, энергия которых отсчитывается от минимума энергии терма. Способ нахождения волновых функций и энергий колебательных состояний состоит в разложении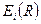вблизи минимума с точностью до членов квадратичных по отклонениям ядер от равновесных положений и диагонализации матрицы кинематических и динамических коэффициентов. Гамильтониан движения ядер при этом переходит в сумму гамильтонианов отдельных нормальных осцилляторов

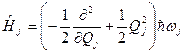, (1.5)

где 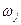- частота, а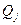-нормальная координата осциллятора, которая представляется в виде разложения по естественным смещениям ядер,

и 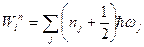, где 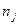-колебательное квантовое число. Волновая функция ядерной подсистемы имеет вид произведения нормальных гармонических осцилляторов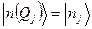. Положение нормальных координат и частот колебаний изменяются при электронном переходе, вследствие чего колебательные волновые функции различных электронных состояний неортогональны, что приводит к образованию вибронных полос поглощения и люминесценции молекул. При необходимости учета ангармоничности колебаний чаще всего используются волновые функции потенциала Морзе.

В случае многоатомных молекул, имеющих большую массу, вращательные степени свободы обычно не учитываются даже в газовой фазе, не говоря уже о конденсированной, где вращение чаще всего невозможно.

Состояния с волновыми функциями 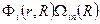называются чисто спиновыми адиабатическими состояниями. Часто такие функции обозначаются как 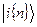или 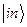. В качестве электронных волновых функций чаще всего используется их выражение при равновесных координатах ядер и пренебрегается их зависимостью от 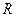(грубое адиабатическое приближение).Приближение, в котором используются такие функции для вычисления матричных элементов взаимодействия различных электронных состояний называется приближением Кондона.

Для дальнейшего изложения удобно ввести оператор неадиабатичности 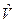, определив его через результат действия на адиабатические функции:

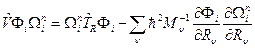. (1,6)

Тогда , где 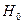называется гамильтонианом адиабатического чисто спинового приближения. Соответствующие функции называются адиабатическими чисто спиновыми и являются базисом для рассмотрения природы молекулярных состояний.