Вращение твердого тела вокруг неподвижной оси

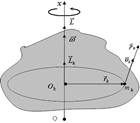
Пусть некоторое твердое тело вращается вокруг неподвижной оси 0 х с угловой скоростью 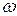. Известно, что вектор 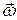в выбранном случае в соответствии с правилом правого винта направлен по оси вращения вверх. Разобьем мысленно это тело на бесконечно большое число бесконечно малых элементов, которые можно рассматривать как материальные точки. Все эти элементы будут описывать окружности, центры которых лежат на оси вращения, с одной и той же угловой скоростью 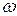. Рассмотрим произвольный k -ый элемент. Его линейная скорость направлена по касательной к окружности радиуса 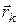и равна 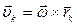. Импульс этой частицы массой 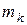: 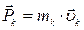. Момент ее импульса 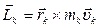. Момент импульса тела равен .

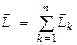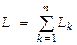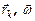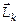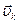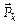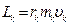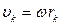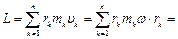
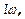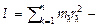Очевидно, что моменты импульса всех частиц будут направлены по оси вращения 0х. Поэтому векторную сумму можно заменить арифметич.: . Векторы (и ), (и ) – взаимно перпендикулярны между собой. Произведем следующие преобразования: ; ; где момент инерции твердого тела относит-но оси0 х ¾ сумма произведений масс всех элементов твердого тела на квадраты их расстояний до оси вращения. Итак, момент импульса со скоростью вращения связан т.о.: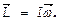

Т.о., в качестве характеристики инертности при вращательном движении материальной точки (МТ) или твердого тела используется не масса (или не просто масса), а момент инерции. Моментом инерции МТ относительно оси вращения называют произведение массы этой точки на квадрат расстояния от оси: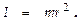

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная суммепроизведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси: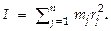

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: 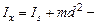момент инерции тела относительно произвольной оси x равен сумме момента его инерции 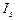относит-но параллель­ной оси, проходящей ч/з центр масс тела, и произведения массы m тела на квадрат расстояния d между осями.

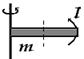
Пример применения теоремы Штейнера: момент инерции прямого тонкого стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец ( эта ось отстоит на d = l /2 от оси, проходящей через центр стержня ): 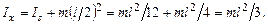Т.о., величина момента инерции зависит от выбора оси вращения.

Кинетическаяэнергиявращения

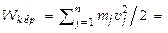
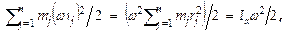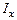АТТ вращается около неподвижной оси проходящей через него. Все точки движутся с одинаковой угловой скоростью w. Кинетич. энергия тела: где — момент инерции тела относительно оси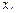

Если АТТ совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна сумме кинетических энергий: 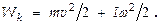Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что в качестве меры инертности при вращательном движении выступает момент инерции тела.

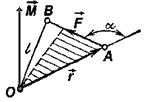
Моментом силы 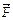относительно неподвижной точки О называется физическая величина 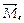определяемая векторным произведением радиуса-вектора 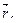проведенного из точки О в точку А приложения силы, на силу 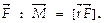Модуль момента силы: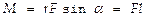 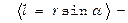плечо силы — кратчайшее расстояние между линией действия силы и точкой О, 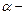угол между вектором силы и радиус-вектором (cм. риc.).

Момент силы относительно неподвижной осиx — скалярная величина M _x равная проекции на эту ось вектора 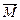момента силы, определенного относит-но произвольной точки О данной оси x. Значение момента M _x не зависит от выбора положения точки О на оси x.

2-ойзаконНьютона для вращательногодвижения. Если ось вращения проходит ч/з центр масс, то имеет место векторное равенство 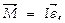где 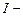главный момент инерции тела (момент инерции относительно оси, проходящей ч/з центр масс). 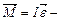выражение 2-ого закона Ньютона для вращат. движения ( уравнение динамики вращат. движения ) .

Моментом импульса (количества движения) материальной точки А относит-но неподвижной точки О называется физическая величина, определяемая векторным произведением: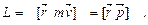

Моментом импульса относит-но неподвижной осиx называют скалярную величину 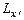равную проекции на эту ось вектора момента импульса, определенного относит-но произвольной точки Оданной оси. Значение момента импульса 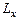не зависит от положения точки Она оси x.

При вращении АТТ вокруг неподвижной оси каждая точка тела движется по окружности постоянного радиуса 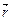со скоростью 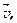перпендикулярной радиусу. Момент импульса отдельной частицы равен 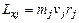и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости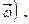

Момент импульса твердого тела относит-но оси есть сумма моментов импульса отдельных частиц:

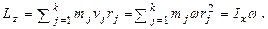
Используя величину момента импульса, основное уравнение динамики вращат. движения твердого тела м-но выразитьтаким соотношением: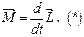

В замкнутой системе момент внешних сил равен нулю: 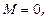следовательно, из ур-ния (*) ¾ 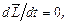т.е. 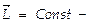закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. Это — фундаментальный закон природы. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.

При равномерном вращении твердого тела относительно некоторой оси х закон сохранения момента импульса 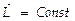равносилен соотношению 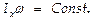Т.о., если в нек-рой вращающейся системе изменить момент инерции (к.-л. образом «за счет внутреннего усилия» деформировать вращающееся тело), должна измениться и угловая скорость его вращения.