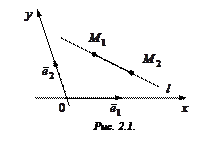 Пусть
Пусть 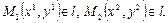 Тогда в качестве направляющего вектора прямой
Тогда в качестве направляющего вектора прямой  можно взять вектор
можно взять вектор 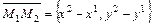
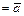 . Так как
. Так как 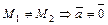
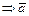 – действительно направляющий вектор прямой
– действительно направляющий вектор прямой  . Положим
. Положим 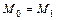 . Тогда из (1.4)
. Тогда из (1.4)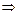
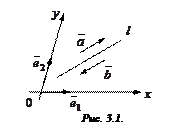
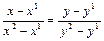 (2.1)
(2.1)
Соотношение (2.1) – уравнение прямой, проходящей через две точки.
Допустим, что 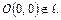 Тогда
Тогда 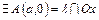 и
и 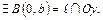 Следовательно, взяв в качестве направляющего вектора вектор
Следовательно, взяв в качестве направляющего вектора вектор 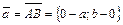 и точку
и точку 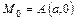 , из (2.1) получим
, из (2.1) получим
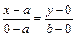 или
или 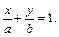 (2.2)
(2.2)
(2.2) – уравнение прямой в отрезках.
Замечание: 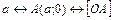 ,
, 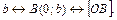
§ 3. УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ. 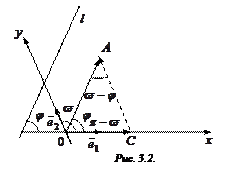
Рассмотрим в аффинной системе координат 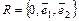 прямую
прямую  , заданную каноническим уравнением
, заданную каноническим уравнением
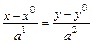 (1.4)
(1.4)
с направляющим вектором 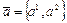 . После несложных преобразований оно принимает вид
. После несложных преобразований оно принимает вид
(1.4) 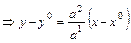
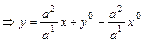 .
.
Определение. Отношение второй координаты направляющего вектора 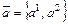 прямой
прямой  к его первой координате называют угловым коэффициентом прямой и обозначают
к его первой координате называют угловым коэффициентом прямой и обозначают
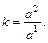 (3.1)
(3.1)
Если обозначить 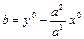 , то уравнение прямой принимает вид
, то уравнение прямой принимает вид
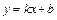 . (3.2)
. (3.2)
Соотношение (3.2) – уравнение прямой с угловым коэффициентом.
Теорема 3.1. Угловой коэффициент прямой не зависит от замены направляющего вектора этой прямой.
▼ Пусть 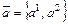 – направляющий вектор прямой и векторы
– направляющий вектор прямой и векторы 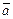 и
и 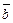 коллинеарны. Тогда
коллинеарны. Тогда
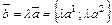 .
.
Следовательно,
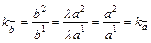
▲ ò
Теорема 3.2. Угловой коэффициент прямой волне определяется углом наклона прямой к оси абсцисс.
▼ôПусть 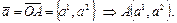
1) т.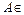 I четверти, следовательно
I четверти, следовательно 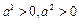 . (*)
. (*)
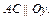

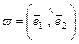 .
.
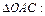
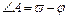
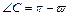 .
.
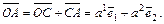
ó∆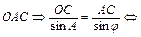
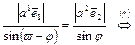
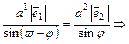
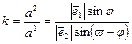 . (3.3)
. (3.3)
2) т.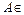 II четверти, следовательно
II четверти, следовательно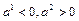 . (**)
. (**)
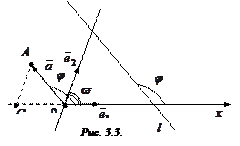 ∆
∆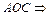
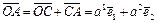 .
. 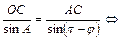
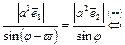
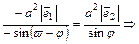
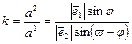 . (3.3)
. (3.3)
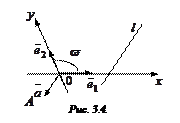
|
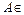 III четверти, следовательно
III четверти, следовательно 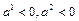 (Рис. 3.4). В силу теоремы 3.1 направляющий вектор
(Рис. 3.4). В силу теоремы 3.1 направляющий вектор 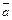 заменим на вектор
заменим на вектор 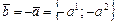 . Тогда
. Тогда 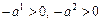 . Поэтому, как и в случае 2), приходим к соотношению (3.3).
. Поэтому, как и в случае 2), приходим к соотношению (3.3).
4) т. 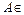 IV четверти, поэтому
IV четверти, поэтому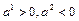 . Тогда в силу теоремы 3.1 направляющий вектор
. Тогда в силу теоремы 3.1 направляющий вектор 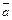 заменим на вектор
заменим на вектор 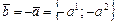 . Тогда
. Тогда 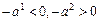 . И, как и в случае 2), приходим к соотношению (3.3).
. И, как и в случае 2), приходим к соотношению (3.3).
Таким образом, из (3.3) следует, что
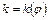 . (3.4)
. (3.4)
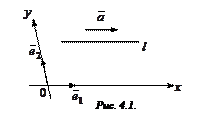 Следствие. В прямоугольной декартовой системе координат угловой коэффициент прямой равен тангенсу угла ее наклона к положительному направлению оси абсцисс.
Следствие. В прямоугольной декартовой системе координат угловой коэффициент прямой равен тангенсу угла ее наклона к положительному направлению оси абсцисс.
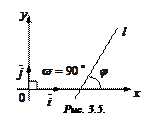 Действительно, так как
Действительно, так как 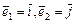 , то из (3.3) получаем
, то из (3.3) получаем
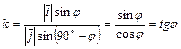 .
.
Таким образом, действительно в прямоугольной декартовой системе координат
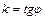 . (3.5)
. (3.5)
§ 4. ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ.
Во всех рассмотренных уравнениях прямой переменные 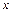 и
и 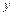 присутствуют только в первой степени. Это говорит о том, что прямая линия определяется уравнением первой степени относительно переменных
присутствуют только в первой степени. Это говорит о том, что прямая линия определяется уравнением первой степени относительно переменных 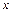 и
и 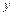 .
.
Справедливо и обратное утверждение.
Теорема 4.1. Всякое уравнение первой степени
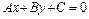 . (4.1)
. (4.1)
при условии
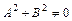 (4.2)
(4.2)
в аффинной системе координат 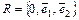 определяет некоторую прямую.
определяет некоторую прямую.
▼ 1) Если 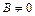 , то (4.1)
, то (4.1) 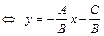 ; положив
; положив 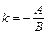 (*) и
(*) и 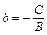 , получаем уравнение
, получаем уравнение 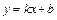 прямой с угловым коэффициентом.
прямой с угловым коэффициентом.
2) Если 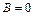 , то (4.1)
, то (4.1)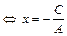 ; положив
; положив 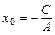 , получаем уравнение
, получаем уравнение 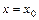 прямой, параллельной оси
прямой, параллельной оси 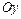 .
.
▲
Замечание. Сравнивая равенство (*) из доказательства теоремы и соотношение (3.1), можно сделать вывод, что направляющий вектор прямой (4.1) имеет координаты ò
ì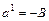 и
и 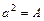 ,
, 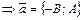 . (4.3)
. (4.3)
Соотношение (4.1) называют общим уравнением прямой.
Частные случаи расположения прямой, заданной общим уравнением, относительно системы координат:
1) 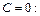 (4.1)
(4.1) 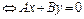
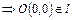 , т.е. прямая проходит через начало координат.
, т.е. прямая проходит через начало координат.
2) 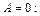 (4.1)
(4.1) 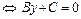
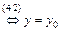 (
(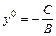 )
)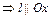 .
.
Действительно, 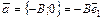 , т.е.
, т.е. 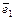 и
и 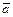 коллинеарны.
коллинеарны.
3) 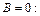 (4.1)
(4.1) 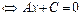
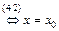 (
(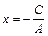 )
) 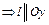 .
.
Действительно, 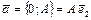 ,
, 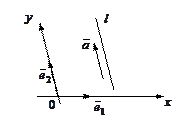 т.е.
т.е. 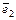 и
и 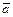 – коллинеарны.
– коллинеарны.
4) 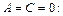 (4.1)
(4.1)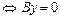
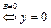
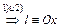 .
.
5) 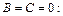 (4.1)
(4.1)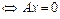
|
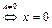
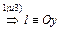 .
.
 2014-02-09
2014-02-09 760
760








