Пусть две прямые 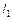 и
и 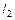 относительно общей декартовой системы координат
относительно общей декартовой системы координат 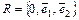 заданы общими уравнениями
заданы общими уравнениями
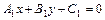 (
(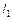 ) (5.1)
) (5.1)
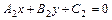 (
(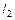 )
)
Из (5.1) 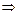
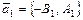 и
и 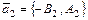 .
.
Очевидно, что прямые 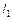 и
и 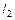 могут занимать на плоскости относительно друг друга одно из трех различных положений:
могут занимать на плоскости относительно друг друга одно из трех различных положений:
1. 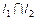 , т.е.
, т.е. 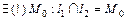 ;
;
2. 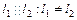 ;
;
3. 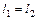 .
.
Рассмотрим эти случаи по отдельности:
1. 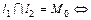
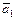 и
и 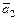 – не коллинеарны,
– не коллинеарны, 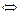
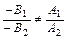
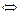
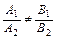 (5.2)
(5.2)
Таким образом, если прямые 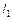 и
и 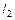 пересекаются, то в их общих уравнениях коэффициенты при неизвестных не пропорциональны.
пересекаются, то в их общих уравнениях коэффициенты при неизвестных не пропорциональны.
Замечание: (5.2) 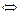
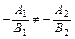 ,
,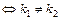 . (5.3)
. (5.3)
Следовательно, если прямые 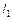 и
и 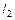 , заданные уравнениями с угловыми коэффициентами, пересекаются, то их угловые коэффициенты не равны.
, заданные уравнениями с угловыми коэффициентами, пересекаются, то их угловые коэффициенты не равны.
С другой стороны, если 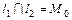 , то система (5.1) имеет единственное решение. А это означает, что ее определитель
, то система (5.1) имеет единственное решение. А это означает, что ее определитель
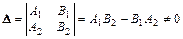
и 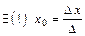 ,
, 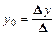 , т.е.
, т.е.  .
.
2. 
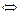
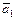 и
и 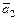 – коллинеарны и если
– коллинеарны и если 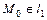 , то
, то 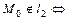
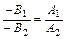
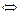
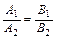
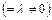 (5.4)
(5.4)
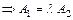 и
и 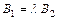 .
.
Пусть 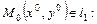
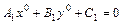
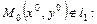
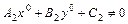
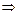
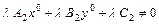
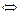
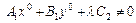
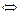
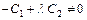
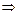
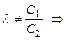
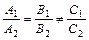 . (5.5)
. (5.5)
Таким образом, если прямые 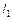 и
и 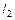 параллельны и не совпадают, то коэффициенты при неизвестных в их общих уравнениях пропорциональны, а свободные члены – не пропорциональны.
параллельны и не совпадают, то коэффициенты при неизвестных в их общих уравнениях пропорциональны, а свободные члены – не пропорциональны.
3. 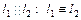
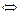
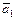 ,
,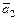 – коллинеарны и если
– коллинеарны и если 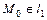 , то
, то 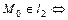
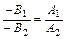
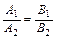
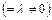
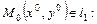
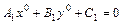
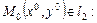

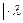
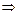
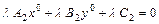
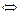
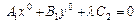
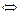
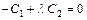
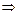
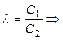
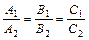 . (5.6)
. (5.6)
Таким образом, если прямые 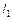 и
и 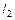 совпадают, то в общих уравнениях этих прямых все соответствующие коэффициенты пропорциональны.
совпадают, то в общих уравнениях этих прямых все соответствующие коэффициенты пропорциональны.
Замечание: (5.6) 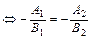 и
и 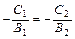 , т.е.
, т.е.
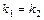 и
и 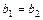 . (5.7)
. (5.7)
Следовательно, если прямые 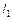 и
и 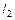 заданы уравнениями с угловыми коэффициентами и совпадают, то справедливы соотношения (5.7).
заданы уравнениями с угловыми коэффициентами и совпадают, то справедливы соотношения (5.7).
 2014-02-09
2014-02-09 498
498








